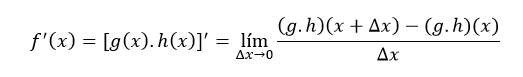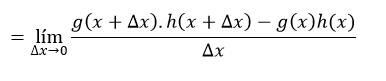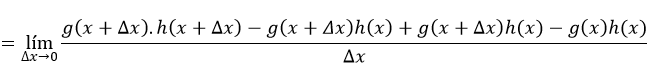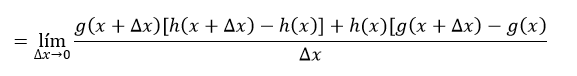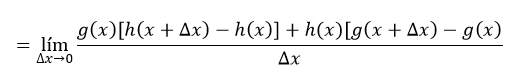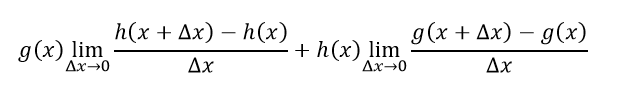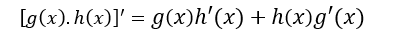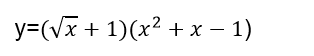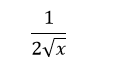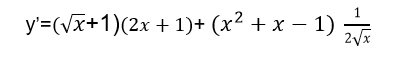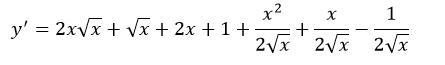
En este post queremos deducir la técnica para derivar el producto de las funciones de variable real continuas y diferenciables, g y h.
In this post we want to deduce the technique for deriving the product of the continuous and differentiable real variable functions, g and h.
Inicialmente, vamos a deducir esa técnica usando la definición formal de derivada. // Initially, let's deduce that technique using the formal definition of a derivative.
Esto es:// This is
Dadas las funciones g y h, con dominio en R (el conjunto de los números reales), se quiere determinar y aplicar en ejemplos la técnica para derivar la función f definida por f(x)=g(x).h(x).
Given the functions g and h, with dominance in R (the set of real numbers), we want to determine and apply in examples the technique to derive the function f defined by f(x)=g(x).h(x).
Comencemos // Let's start
Sabemos que la derivada de una función f en cualquier punto de su dominio está dada por:// We know that the derivative of a function f at any point in its domain is given by:
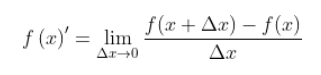
Pero, en nuestro caso particular, f(x) esta definida como un producto de dos funciones g y h, así: f(x)=g(x)/h(x).
But, in our particular case, f(x) is defined as a product of two functions g and h, like this: f(x)=g(x)/h(x).
Por lo tanto, dicha definición adecuada a la definición de f es esta:// Therefore, such a definition appropriate to the definition of f is this:
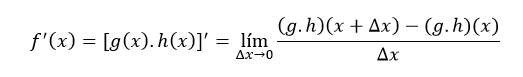
Aplicando la definición de producto de funciones, la expresión anterior queda así:// Applying the definition of a feature product, the above expression looks like this:
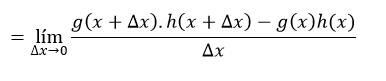
Sumando y restando en el numerador // Adding and subtracting in the numerator g(x+Δx)h(x)
El resultado es este:// The result is this:
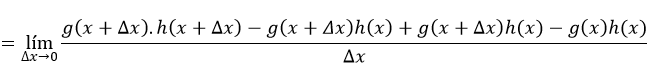
Sacando factor común, va resultando esto:// Finding a common factor, the result is this:
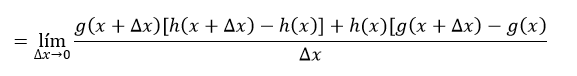
Como g es continua y Δx→0, then: //Since g is continuous and Δx→0, then:
g(x+ Δx)=g(x)
De tal manera, que nuestra expresión toma la siguiente forma:// Thus,our expression takes the following form:
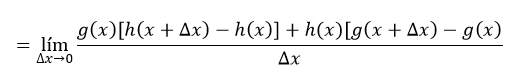
Separando en suma de fracciones y aplicando los teoremas de límites, nos queda así:// Separating the sum of fractions and applying the limit theorems,we get as follows:
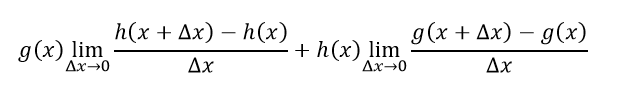
Lo cual se reduce a:// Which boils down to:
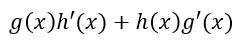
De donde:// Where from:
 |
Lo cual, es la fórmula que estábamos buscando. // Which, is the formula we were looking for.
¿Cómo se aplica esta fórmula? // How is this formula applied?
Veamos un ejemplo:// Let's look at an example:
Hallar la derivada de:// Find the derivative of:
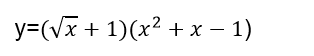
Aquí se nos está solicitando que derivemos a la función ''y'', la cual es el producto de dos funciones, ellas son:
Here we are being asked to derive the function ''y'', which is the product of two functions, which are:
La primera función es √x+1 y la segunda es (x2+x-1) // The first function is √x+1 and the second is (x2+x-1)
Ahora, vamos a aplicar la fórmula, en tal sentido, derivemos la primera de las funciones.// Now, let's apply the formula, in that sense, let's derive the first of the functions.
Es decir, (√x+1)', cuyo resultado es:// That is,(√x+1)', the result of which is: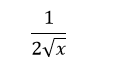 
Y luego, la segunda: (x2+x-1)', cuyo resultado es:// And then the second one: ( x2+x-1)', the result of which is: 2x+1
Sustituyamos estos resultados en la fórmula de la derivada de un producto:// Let's substitute these results into the formula of the derivative of a product:
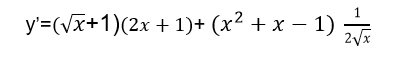
De donde:// Where from:
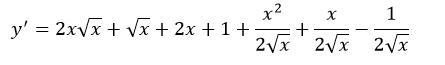
Lo cual es el resultado deseado:// Which is the desired result:
A continuación, dejo algunas actividades para el lector, cualquier duda puede ser planteada a través de los comentarios, con gusto responderé.
Below, I leave some activities for the reader, any questions can be raised through the comments, I will gladly answer.
Hallar la derivada de:// Find the derivative of:
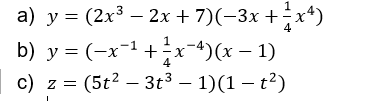
Créditos
El texto es original de la autora, la image es de Pixabay.
El texto es original de la autora, la image es de Pixabay.
Credits
The text is original by the author, the image is from Pixabay.
The text is original by the author, the image is from Pixabay.