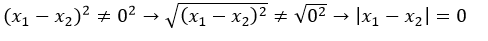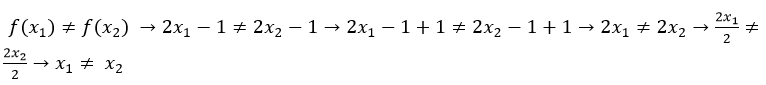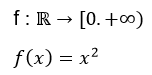
Funciones Inyectivas, Sobreyectivas y Biyectivas /// Injective, Overjective and Bijective Functions

@analealsuarez · 2023-12-14 01:23 · entropia

image.png

### Funciones Biyectivas
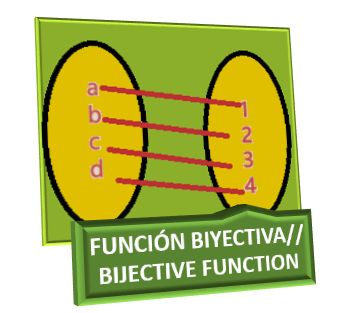
A continuación, es este post, vamos a tratar el tema de las funciones biyectivas. La palabra biyectiva, en matemática, se usa para calificar a un tipo de función que cumple dos cualidades previas, estas son: inyectividad y sobreyectividad.
Es bueno aclarar antes de comenzar, que debemos tener en cuenta cuáles son: el conjunto de partida y el conjunto de llegada de la función que vamos a considerar, en nuestro caso, vamos a tratar con funciones cuyo conjunto de partida y de llegada es R.
### Bijective Functions
Next, in this post, we are going to deal with the topic of bijective functions. The word bijective, in mathematics, is used to qualify a type of function that meets two previous qualities, these are: injectivity and overjectivity. It is good to clarify before starting, that we must take into account which are: the set of departure and the set of arrival of the function that we are going to consider, in our case, we are going to deal with functions whose set of departure and set of arrival is R.

|

image.png
### ¿Entonces, que es inyectividad? #####
Una función se dice que es inyectiva si a cada par de elementos diferentes *x*1 y *x*2 del dominio de dicha función se le hace corresponder dos imágenes diferentes *y*1 y *y*2 en su recorrido.
### So, what is injectivity? #####
A function is said to be injective if each pair of different elements *x*1 and *x*2 in the domain of that function is matched by two different images *y*1 y *y*2 in its path.
Por ejemplo, si tenemos la función f(x)=x2 y queremos verificar si es inyectiva, solo debemos tomar dos pares de valores para la x, por ejemplo:
For example, if we have the function f(x)=x2 and we want to verify if it is injective, we only have to take two pairs of values for x, for example:

|

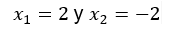
image.png
Luego evaluaremos la función para estos dos valores y obtendremos lo siguiente:
We will then evaluate the function for these two values and obtain the following:

|

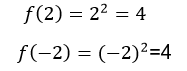
image.png
De tal forma que para dos valores diferentes de x obtenemos la misma imagen, lo cual contradice a definición de inyectividad.
Thus, for two different values of x we obtain the same image, which contradicts the definition of injectivity.
###### Pero, vamos a demostrarlo:
###### But, let's prove it:
Tomemos dos valores cualesquiera en el dominio de f: x1 y x2 tal que x1 ≠ x1, y probemos que f no es inyectiva.

Let us take any two values in the domain of f:x1 and x2 such that x1 ≠ x2 , and prove that f is not injective.

###### Comencemos:
###### Let's get started:
Procederemos por reducción al absurdo, asumiremos una hipótesis que consideramos verdadera y luego llegamos a la contradicción de la misma.
We will proceed by reductio ad absurdum, we will assume a hypothesis that we consider true and then we arrive at the contradiction of the hypothesis.
Sabemos por la hipótesis inicial que x1 ≠ x2 entonces x1 - x2≠0, apliquemos la función a ambos miembros de la igualdad: f(x1 - x2) ≠ f(0), esto significa que:

We know from the initial hypothesis that x1 ≠ x2 so x1 - x2≠0, let's apply the function to both members of the equality: f(x1 - x2) ≠ f(0), this means that:

|

image.png
Para que esta igualdad se cumpla es necesario que:x1 - x2 =0 , de donde: x1 = x2

For this equality to be fulfilled it is necessary that:x1 - x2 =0 , from which: x1 = x2

Lo cual contradice la hipótesis inicial donde suponíamos que:x1 ≠ x2

Which contradicts the initial hypothesis where we assumed that: x1 ≠ x2

Con este resultado podemos afirmar que esta función f(x)=x2, no es inyectiva.

With this result we can affirm that this function f(x)=x2 is not injective.

Veamos ahora con este otro ejemplo:
Let's see now with this other example:
###### Probar que la función f(x)=2x-1 es inyectiva.
###### Prove that the function f(x)=2x-1 is injective.
Comencemos tomando dos valores cualesquiera en el dominio de f: x1 y x2 tal que x1 ≠ x2
Let's start by taking any two values ​​in the domain of f: x1 and x2 such that x1
Apliquemos la función f a ambos miembros de la igualdad:
Let's apply the function f to both members of the equality:
image.png
Con lo cual llegamos a lo que queríamos demostrar.
With which we arrive at what we wanted to demonstrate.
### Veamos ahora Función Sobreyectiva Una función f es sobreyectiva si ∀y ϵ Rec(f) ∃ x ϵ Dom(f) tal que f(x)=y
### Let's now see Surjective Function A function f is surjective if ∀y ϵ Rec(f) ∃ x ϵ Dom(f) such that f(x)=y
Veamos si la función f(x)=x2 es sobreyectiva:
Let's see if the function f(x)=x2 is surjective:
Para que esta función sea sobreyectiva debemos asegurarnos de que todo y en el Rec(f) debe ser imagen de algún x en el Dom(f); para verificar esto haremos lo siguiente:
Primero tomaremos y en el Rec(f), eso significa que y=x2≥0, lo cual evidencia que los números reales negativos no pertenecen al recorrido de esta función, en tal sentido existen números reales en el conjunto de llegada que no pertenecen al recorrido de esta función, es por ello que afirmamos que f no es sobreyectiva.
For this function to be surjective we must ensure that every y in the Rec(f) must be the image of some x in the Dom(f); To verify this we will do the following:
First we will take y in the Rec(f), that means that y=x2≥0, which shows that negative real numbers do not belong to the route of this function, in this sense there are real numbers in the arrival set that do not belong to the route of this function, which is why we affirm that f is not surjective.
Pero si la redefinimos así:
But if we redefine it like this:

|

image.png
En este caso si es sobreyectiva ya que el conjunto de llegada es igual al recorrido de la función.
In this case it is surjective since the arrival set is equal to the path of the function.
### Ejercicio para el lector
Verificar que f(x)=2x-1 es sobreyectiva.
### Exercise for the reader
Verify that f(x)=2x-1 is surjective.
###### Finalmente, cuando una función cumple las dos condiciones anteriores, se dice que es biyectiva. Es decir, una función es biyectiva si y solamente si es inyectiva y sobreyectiva a la vez. En los dos ejemplos anteriores, f(x)=2x-1 es biyectiva y f(x)=x2 no es biyectiva.
###### Finally, when a function meets the two previous conditions, it is said to be bijective. That is, a function is bijective if and only if it is injective and surjective at the same time. In the two examples above, f(x)=2x-1 is bijective and f(x)=x2 is not bijective.

image.png

#### Créditos
El texto es original de la autora, una de las imágenes es de Pixabay y la otra con la ayuda de Paint.
#### Credits
The text is original by the author, one of the images is from Pixabay and the other with the help of Paint..
#entropia #education #stem-espanol #ocd #ocdb #stemsocial #spanish
Payout: 0.000 HBD
Votes: 259
More interactions (upvote, reblog, reply) coming soon.