Este post lo vamos a dedicar a las operaciones con funciones, es decir: adición, sustracción, multiplicación y división de funciones.
This post is going to be dedicated to operations with functions, that is: addition, subtraction, multiplication and division of functions.
Veamos:
Sean f y g dos funciones cualesquiera con sus respectivos: Dom(f), Dom(g)
Sean f y g dos funciones cualesquiera con sus respectivos: Dom(f), Dom(g)
Let's see:
Let f and g be any two functions with their respective functions: Dom(f), Dom (g)
Let f and g be any two functions with their respective functions: Dom(f), Dom (g)
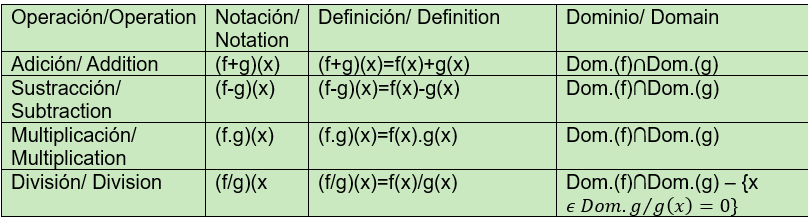
Definimos:
We define:
 |
||
|---|---|---|
Veamos algunos ejemplos: // Let's look at some examples:
Si: // If:
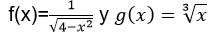
Hallar:
f+g, f-g, f.g y f/g con sus dominios. // Find: f+g, f-g, f.g and f/g with their domains.
##### Solución:
---
### Primero hallemos los dominios de f y g respectivamente:
Por lo tanto, corresponde resolver esa desigualdad cuadrática
La función f está definida mediante un cociente, esto significa que debemos excluir los valores de x que hacen que el denominador √(4-x2 ) sea igual a 0, es decir: 2 y -2. Por otro lado, 4-x2 deberá ser positiva para que pueda existir su raiz cuadrada en R, es decir, para que sea un número real; de tal forma que la cantidad subradical de √(4-x2 ), es decir : 4-x2, deberá ser mayor que 0; todo lo referido anteriormentte se resuelve afirmando que 4-x2>0.
Por lo tanto, corresponde resolver esa desigualdad cuadrática
##### Solution:
---
### First let's find the domains of f and g respectively:
Therefore, it is necessary to solve this quadratic inequality
The function f is defined by a quotient, this means that we must exclude the values of x that make the denominator √(4-x2 ) equal to 0, that is: 2 and -2. On the other hand, 4-x2 must be positive for its square root to exist in R, that is, for it to be a real number; in such a way that the subradical quantity of √(4-x2), that is: 4-x2, must be greater than 0; Everything mentioned above is resolved by stating that 4-x2>0.
Therefore, it is necessary to solve this quadratic inequality
4-x2>0.
Esto es:// This is:
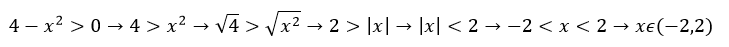
En consecuencia, el Dom(f)= (-2,2)//Consequently, the Dom(f)= (-2,2)
En el caso de la función g estamos tratando con una función definida por una raíz cúbica , este tipo de raíz admite valores positivos y negativos para la x, en consecuencia, el Dom(g)=R.
In the case of the function g we are dealing with a function defined by a cube root, this type of root admits positive and negative values for the x, consequently, the Dom(g)=R.
Representemos en una recta al dominio de estas dos funciones y escojamos la intersección de ambos dominios, es decir: todos aquellos valores de x que se encuentren en ambos dominios, excluiremos los que están en uno y no en el otro dominio.
Let's represent the domain of these two functions on a straight line and choose the intersection of both domains, that is: all those values of x that are in both domains, we will exclude those that are in one and not in the other domain.
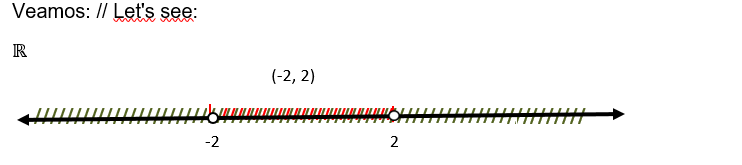
Las líneas verdes representan el dominio de la función g y las líneas rojas representan el dominio de la función f; la intersección de ambos dominios está representado por el cruce de las líneas rojas y verdes, es decir: (-2, 2). Los puntos abiertos indican que -2 y 2 no están en el dominio de f, consecuentemente no están en la intersección.
The green lines represent the domain of the g function and the red lines represent the f function domain; The intersection of both domains is represented by the crossing of the red and green lines, i.e.: (-2, 2). The open points indicate that -2 and 2 are not in the domain of f, therefore they are not in the intersection.
Conclusión:// Conclusion:
Dom(f)∩Dom(g)= (-2, 2)
Vamos ahora con las operaciones:// Now let's go with the operations:

¿Por qué excluimos el 0 en el dominio de la función cociente? /Why do we exclude 0 in the domain of the quotient function?
Ejercicio para el lector:// Exercise for the reader:
Dadas las siguientes funciones: // Given the following functions:

Hallar:// Find
f+g, f-g, f.g y f/g con sus respectivos dominios.// with their respective domains

### Créditos
El texto es original de la autora, una de las imágenes es elaborada con inteligencia artificial y la otra es de Pixabay.
Credits
The text is original from the author, one of the images is created with artificial intelligence and the other is from Pixabay.