Saludos a todos, les doy la más cordial bienvenida a mi blog. Hoy les voy a explicar la suma de fracciones.

Pero, ¿qué es una fracción? En primer lugar, una fracción es un objeto matemático que posee dos partes: el numerador, el cual es el número que está sobre una raya de fracción, y el denominador, es el número que está debajo de la raya de fracción"; es importante destacar que el denominador debe ser diferente de 0.

Una fracción tiene la forma de a/b donde a y b son dos números reales tales que b≠0

• Como por ejemplo tenemos los siguientes: 1/2 y 3/4

El número que esta sobre la raya de fracción se llama ''numerador'' y nos representa el todo que vamos a dividir en partes iguales, el número que está debajo de la raya de fracción es el ''denominador'', este nos dice en cuántas partes vamos a dividir ese todo.

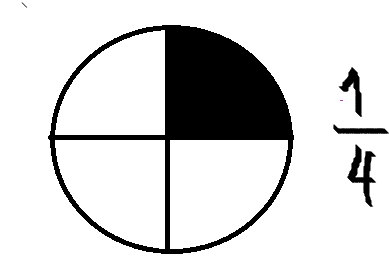
Veamos en la imagen que el todo se ha dividido en 4 partes iguales, de esas partes se ha seleccionado una, la cual queda representada como ¼, es decir, de las 4 partes en que hemos dividido al ‘’todo’’, y de esas partes se ha tomado una.

Existen dos tipos de fracciones, ellas pueden ser: propias e impropias.

Las fracciones propias tienen un numerador menor que el denominador, mientras que las impropias tienen un numerador mayor o igual al denominador."

He aquí un ejemplo de una fracción impropia:

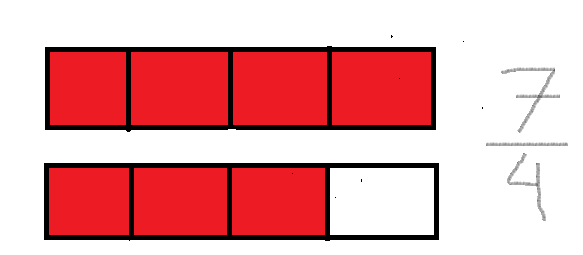
Y aquí un ejemplo de una fracción propia

También tenemos las fracciones mixtas y las fracciones equivalentes. Una fracción es mixta si se puede expresar como una fracción impropia y a su vez como la suma de un numero entero más una fracción propia. En la siguiente imagen conseguimos un ejemplo:

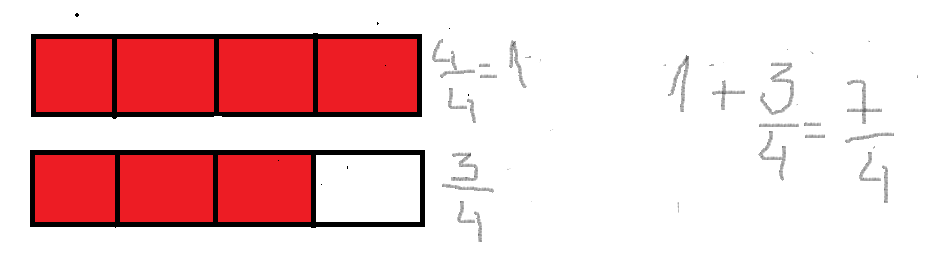
Observación: Más adelante explicaremos con ejemplos las fracciones mixtas.

A continuación, hablaremos acerca de las fracciones equivalentes.

Dos fracciones: a/b y c/d son equivalentes si y solo si se cumple que a.d=b.c A continuación, mostramos algunos ejemplos: 4/3 y 20/15 son equivalente ya que 4.15=3.20.

Esto es: 60=60

(-7)/2 y (-21)/6 son equivalentes ya que-7.6=2.(-21)

En ambos lados de esta igualdad,el resultado es-42.

1/2 y 3/4 no son equivalentes ya que el producto 1.4=4 y el producto 2.3=6

A continuación, vamos a sumar fracciones. Pero, primero hablemos de dos tipos de fracciones especiales, ellas son:

La Fracción Nula La Fracción Nula es aquella fracción cuyo numerador es 0 y su denominador es cualquier número real distinto de 0. Esta fracción se identifica con el número real 0. Esto es: 0/b=0,donde b es diferente de 0. Ejemplos: 0/2=0 0/(-4)=0

La Fracción Unidad La Fracción Unidad, es una fracción cuyo numerador y denominador son iguales. Esta fracción se identifica con el número real 1. Esto es: a/a=1,donde a es diferente de 0. Ejemplos: 3/3=1 (-4)/(-4)=1

Comencemos con la suma de fracciones: Al sumar fracciones se pueden presentar dos casos:

El primero: Sumar fracciones con el mismo denominador En este caso, simplemente se suman los numeradores de acuerdo al signo, es decir, se realiza la suma algebraica de los numeradores y se repite el mismo denominador. Esto es:

Esta regla para sumar fracciones también es válida para la diferencia de fracciones:

Y en general, para la suma algebraica de fracciones con igual denominador:

Para sumar o restar fracciones con diferentes denominadores se procede mediante la siguiente regla:

Pero, ¿existe otro procedimiento para esta operación? Si existe otro procedimiento, y es el siguiente:

Primero se busca el mínimo común múltiplo (m.c.m) entre los denominadores de las fracciones que estamos sumando.

Veamos:

Sigamos con el ejemplo anterior:

Identifiquemos los denominadores y busquemos el m.c.m entre 10 y 12.

Así:

Para obtener el mínimo común múltiplo entre los denominadores, lo que hacemos es multiplicar todos los factores primos que se encuentran en la última columna.

Eso es:

El m.c.m (10 y 12) =2.2.3.5=60

Copiamos nuestro ejercicio anterior y lo igualamos a una nueva fracción cuyo denominador es 60, y luego procedemos de la siguiente manera:

Dividimos 60 entre cada denominador de los sumandos dados, y el resultado de esa división se multiplica por el numerador respectivo:

Así:

60÷10=6 →6.4=24 60÷12=5→5.6=30

Estos dos resultados van sobre la raya de fracción de la nueva fracción, finalmente se efectúa la suma algebraica, así:

Aquí verificamos que nos da el mismo resultado que con el procedimiento anterior.

Y de estas dos formas podemos sumar o restar fracciones con distinto denominador.

Veamos algunos ejemplos misceláneos.

Efectué las operaciones siguientes:

En ejercicios de sumas de este tipo, se multiplica el entero por el denominador de la fracción y el resultado se suma con el numerador respectivo, así:

Cuando se nos presenta una expresión como esta, estamos ante un numero mixto:

Y, ¿a cuánto equivale ese número mixto?

equivale a 10 unidades enteras sumadas con 1/3

Esto es:

Es decir, que un número mixto equivale a la suma de su parte entera con su parte fraccionaria.

Es decir que:

Bueno amigos, espero que les haya resultado útil este post. Hasta una próxima oportunidad.

Créditos:

Este post es totalmente original de la autora.