Let X and Y be a set of real numbers. A real function f of a real variable x from X to Y is a correspondence that assigns to each number x of X exactly one number of y of Y. The domain of f is the set X. The number y is the image of x by f and is denoted by f(x), which is called the value of f at x. The path or range of f is defined as the subset of Y formed by all the images of the numbers of X. All this is explained in the following figure:  Functions can be expressed in multiple ways. However, in this case I only want to explain functions with dependent and independent variables, such as: 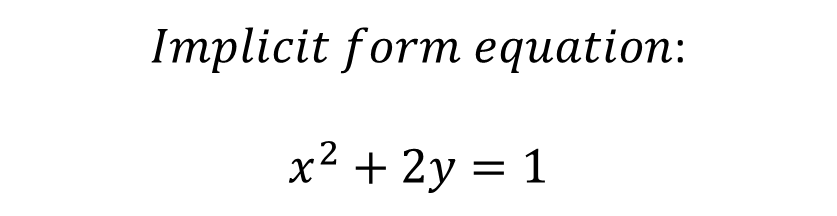 To express in function form, it is convenient to clear y: 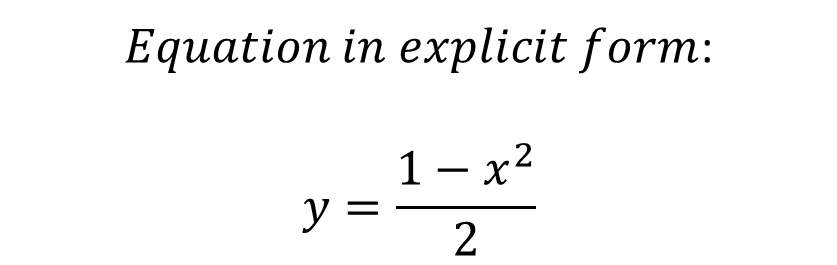 If we use f as the name of the function, then this equation can be written: 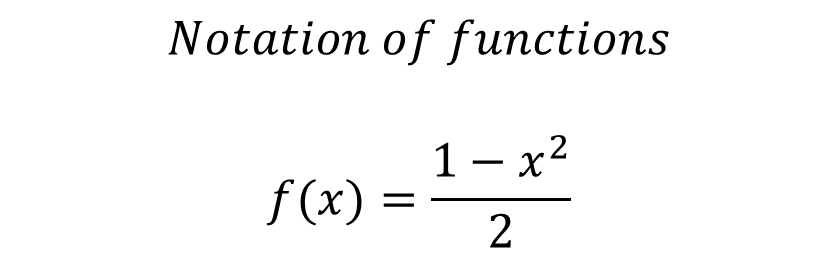 Depending on how a function is denoted or expressed, it is possible to have the advantage of being able to identify the dependent variable as follows ***f(x)***, and at the same time we can express that the independent variable is ***x*** and that the function is denoted by ***"f".*** The symbol ***f(x)*** se lee “f of x”. Function notation has the advantage of saving words, since instead of asking: What is the value of y corresponding to x=3? You can ask in a more summarized form: What is the value of f(3)? We could then state that if we have an equation that defines a function, then the role of the variable ***x*** is simply that of a gap to be filled. For example, the function given by: 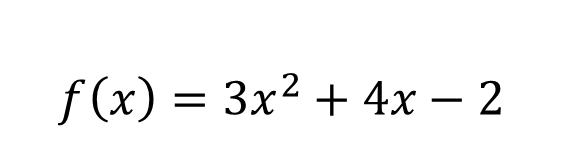 Which can be described as: 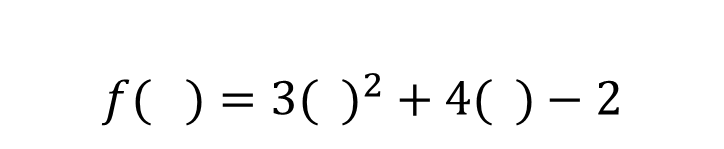 To evaluate such a function considering that we can substitute any real number inside the parenthesis, for example for x = 2, implies that:  It is important to note that although it is very common to use ***f*** as a suitable symbol to denote a function and ***x*** for the independent variable, it should be noted that other symbols can be used without any problem. For example, all of the following equations represent the same function: 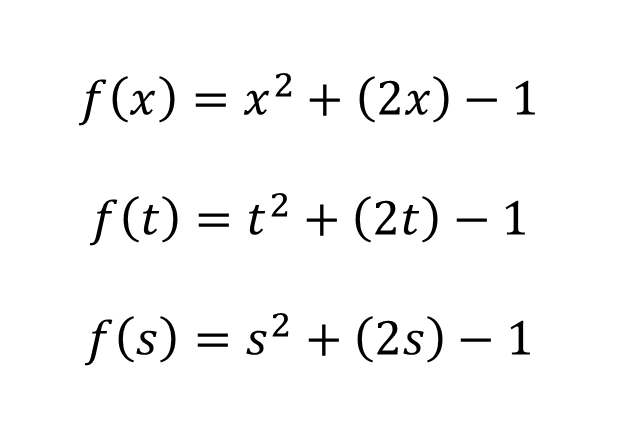 The function is the same, what changes is the independent variable, which for the first case is ***x***, for the second case is ***t*** and for the third case is ***s***. ### ***Bibliographic Reference***
Calculus with Analytic Geometry by Ron Larson, Robert, P. Hostetler and Bruce H. Edwards. Volume I. Eighth Edition. McGraw Hill. Año 2006