Importance of studying density in oil well drilling

.jpg) This is perhaps one of the most common concepts in engineering and in the study of physics and chemistry, since it is not surprising that even a high school student can tell you that density is the ratio between the mass of a substance and its volume. So the difficulty does not lie in understanding this concept, because we can even interpret it with the following equation:  Where ρ is density, m is mass, and V is volume. However, what we may fail to understand is that we can also correctly assume that density is the calculation of the slope of a graph where mass is on the Y-axis and volume is on the X-axis. This variation in mass and volume can occur because the mass and volume occupied by a substance depend on the pressure and temperature to which the substance is subjected. The above leads us to conclude, in part, that in reality there are many substances that vary in density when subjected to different pressures and temperatures. such as drilling fluid (also called drilling mud), which can have a density such that as the well deepens and the pressure and temperature change at the bottom of the well, the density of the drilling fluid also changes. The equation we all know, where density equals mass divided by volume, is only valid as long as the mass remains constant. It is important to mention that the oil industry uses incorrect terminology when referring to density. From my experience in the field, I can tell you that density is referred to as mud weight, which is scientifically incorrect, since if we assume that it is not mass but weight, and we divide it by volume, then that is specific weight, since weight divided by volume is specific weight. ### ***How can density be considered based on whether it is a pure substance or a mixture?***

If we consider a substance to be pure, it is because it has no additives, so its density will be constant, and we can calculate it as mass divided by volume. However, if the substance is a mixture, then we must consider the variability of each substance that makes up the mixture in relation to its mass concentration. In the oil industry, more specifically in well drilling, the drilling fluid used is often a mixture of fluids of different densities, such as water, solid materials such as barite, bentonite, aerated fluids such as nitrogen, air, foam, among others. It is important to study the density and other variables involved in the composition of these fluids, since their density determines the hydrostatic pressure with which the pressure of the fluids contained in the reservoir, such as gas and/or oil, will be withstood at the bottom of the well.  [Image source](https://en.wikipedia.org/wiki/File:US_Navy_111005-N-ZN781-031_Aviation_Boatswain%27s_Mate_(Fuel)_3rd_Class_Rolando_Calilung_tests_for_a_specific_gravity_test_on_JP-5_fuel.jpg) ### ***What happens if only the relative density of a fluid such as oil is known?***

The relative density of a fluid arises from the need to simplify density comparisons between different substances. To this end, the value of the new density, called relative density, was sought to be dimensionless, giving rise to the following equation: 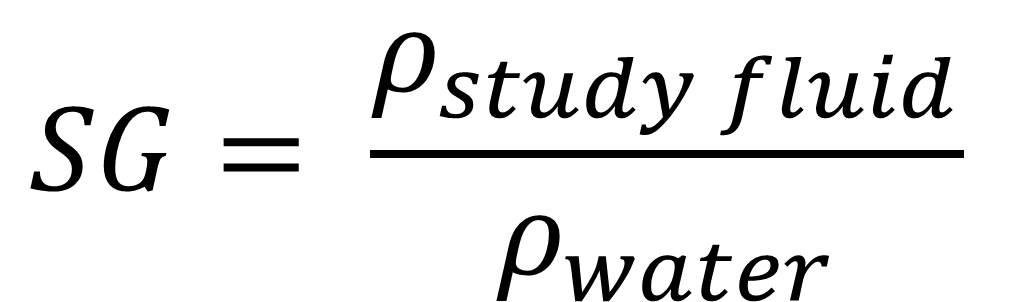 Where SG is the relative density of the fluid, if we analyze the equation, we can see that if we want to know the density of a given fluid only by knowing its relative density, we simply solve for the density of the fluid being studied, which would be equal to the relative density of the fluid (SG) multiplied by the density of water, which is 1000 kg/cubic meter. An example of this is petroleum, which has a relative density that varies depending on whether it is light, medium, or heavy petroleum. Suppose we want to know the density of a light oil that has a relative density equal to 0.83. We solve for the density of the fluid under study, which in this case is light oil with a relative density of 0.83, and we are left with: 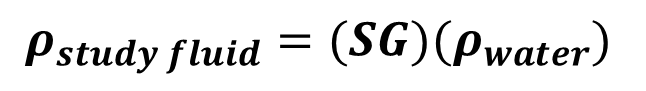 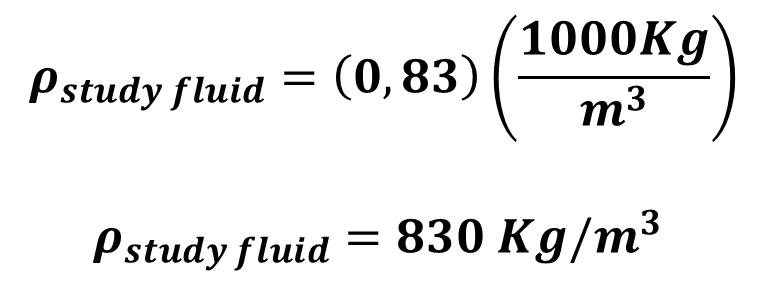 So we conclude that oil with a relative density of 0.83 will have a density of 830 kg/cubic meter. To calculate the relative density of a liquid fluid, always divide the density of the liquid fluid by the density of water. However, if you are calculating the relative density of a gaseous fluid, you will always divide the density of the gaseous fluid by the density of air. The importance of relative density in the oil industry is that it allows the quality of a type of oil to be standardized based on the quality of the oil in a way that is not complicated, as it is dimensionless. ### ***Can other calculations be obtained from density based on other variables?***

If other calculations can be obtained from the density of a substance, in well drilling we have the example of drilling fluid, where simply by knowing the density of the fluid we can know the pressure gradient measured in psi/foot. To do this, it is important to use the hydrostatic pressure equation for drilling fluid: Ph = (0.052)(density of drilling fluid)(h=height of fluid column) If we solve for (0.052)(density of drilling fluid) = Ph / h Therefore, Ph / h becomes the pressure gradient, thus: Hydrostatic pressure gradient of the drilling fluid = 0.052 x Density of the drilling fluid measured in pounds / gallons. Example: You have a drilling fluid with a density of 9 pounds/gallon. Calculate the hydrostatic pressure gradient. - Hydrostatic pressure gradient = 0.052 x 9 pounds/gallon - Hydrostatic pressure gradient = 0.468 psi/foot. The importance of knowing the hydrostatic gradient is that you can know the hydrostatic pressure that the drilling fluid will exert at any depth of the well as long as the density of the drilling fluid remains the same. For example: calculate the pressure exerted by the fluid of 0.468 psi/ft at a depth of 6000 ft. Hydrostatic pressure = Hydrostatic pressure gradient x Depth Hydrostatic pressure = 0.468 psi/ft x 6,000 ft Hydrostatic pressure = 2,808 psi This means that at a gradient of 0.468 psi/foot and a well depth of 6,000 feet, the drilling fluid will exert a hydrostatic pressure of 2,808 psi. It is also important to note that as the depth of the well increases, the hydrostatic pressure at the bottom will increase, even though the hydrostatic pressure gradient remains the same. ### ***References***

[Density](https://en.wikipedia.org/wiki/Density) [Relative density](https://en.wikipedia.org/wiki/Relative_density) [Density of Petroleum](https://hypertextbook.com/facts/2007/ArtemGindin.shtml#:~:text=Petroleum%20is%20used%20mostly%20by,Artem%20Gindin%20%2D%2D%202007)