[1] The graph of an equation in x and y is symmetric about the y-axis if substituting x for -x in the equation yields an equivalent equation. [2] The graph of an equation in x and y is symmetric about the x-axis if substituting y for -y in the equation results in an equivalent equation. [3] The graph of an equation in x and y is symmetric about the origin if substituting x for -x and y for -y in the equation yields an equivalent equation. There is an additional strategy to know if a graph is symmetric with respect to the y-axis, for example the graph of a polynomial is symmetric with respect to the y-axis if each of the terms of the polynomial has even exponent (or is a constant), for example the following polynomial: 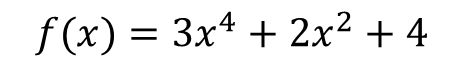 The polynomial function shown is symmetric about the y-axis. The counterpart is when a polynomial function has all its terms with odd exponent, that means that it is symmetric with respect to the origin, as for example:  ### ***Symmetry exercises***
From exercises 19 to 26 of Larson's calculus book I am going to do exercise 27 of section P.I on page 8. Find if the following function is symmetric with respect to the coordinate axes and the origin:  We test to see if there is symmetry with respect to the y-axis: It must be satisfied that: f(-x) = f(x) Therefore: 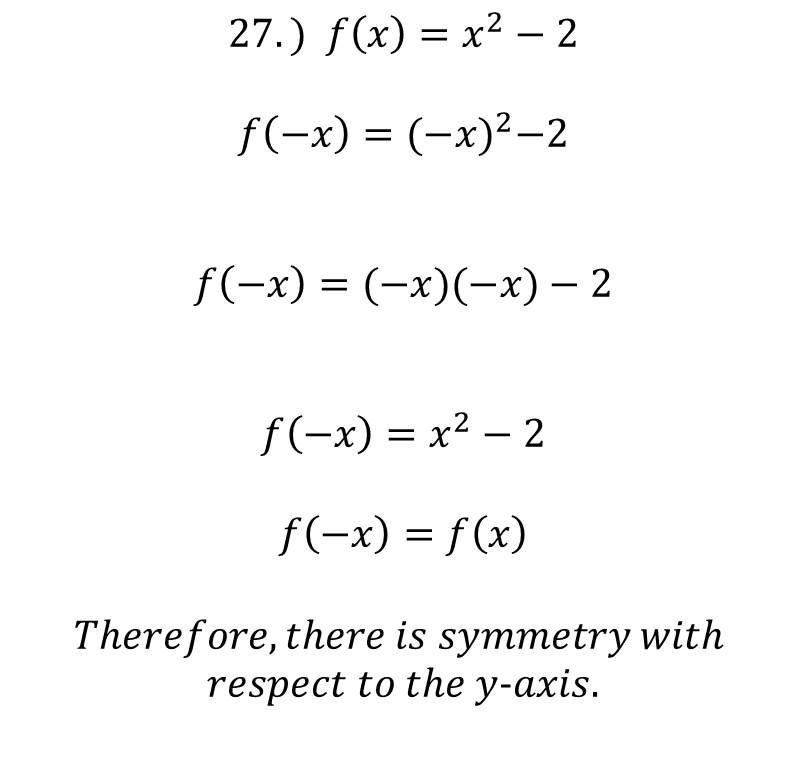 We test to see if there is symmetry with respect to the x-axis: It has to be fulfilled that: -f(x) = f(x) Therefore: 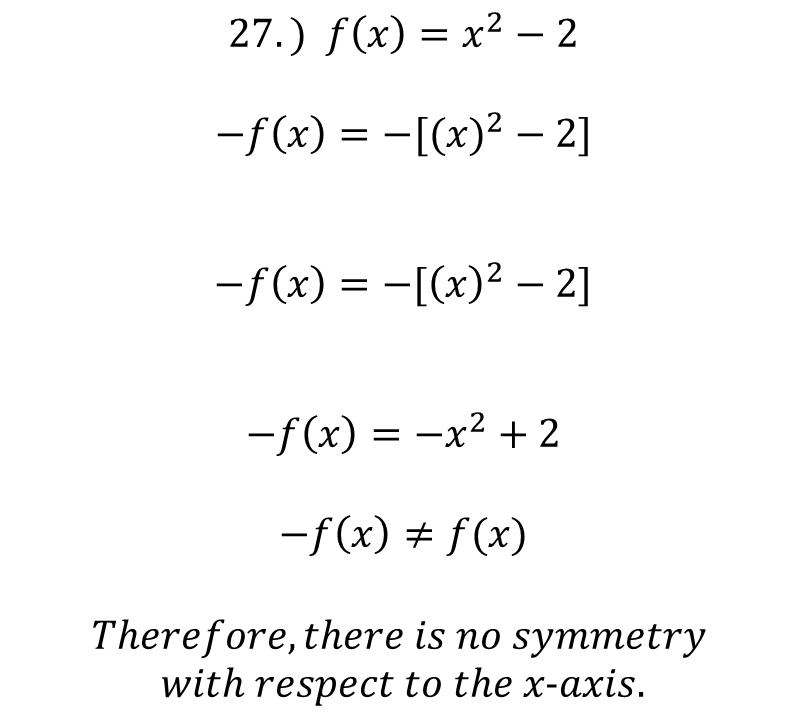 We test to see if there is symmetry with respect to the origin: It must be fulfilled that: -f(x)=f(-x) must be equal to f(x) Therefore:  The conclusion of the case is that the function is only symmetric with respect to the y-axis, it has no symmetry with either the x-axis or the origin. We can corroborate this with the following graph in Geogebra: 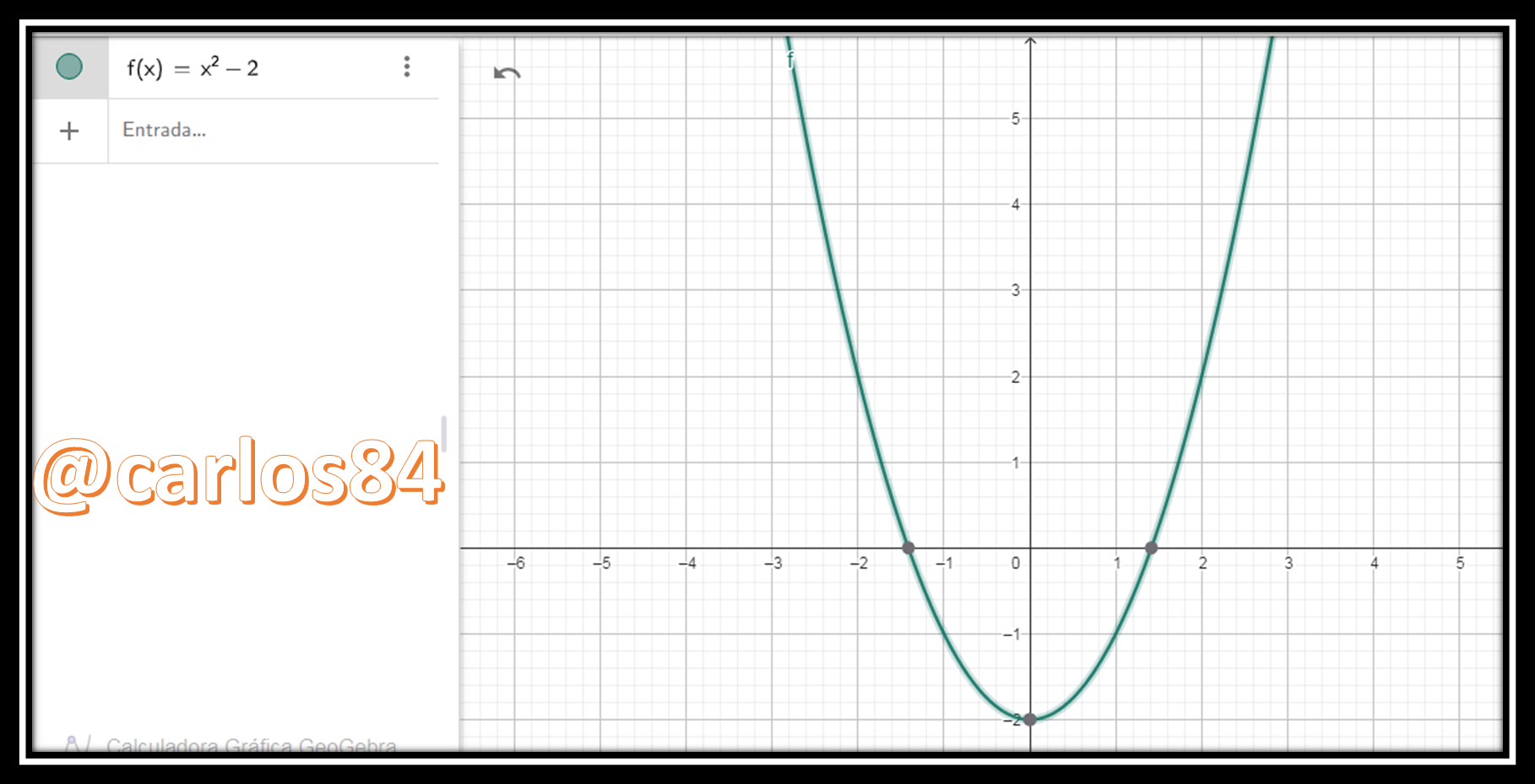 ### ***Bibliographic Reference***
Calculus with Analytic Geometry by Ron Larson, Robert, P. Hostetler and Bruce H. Edwards. Volume I. Eighth Edition. McGraw Hill. Año 2006