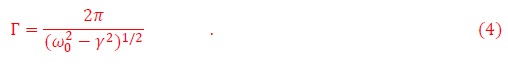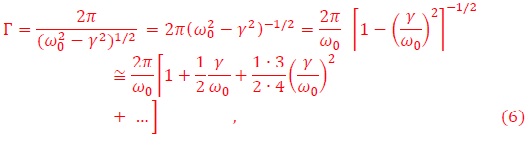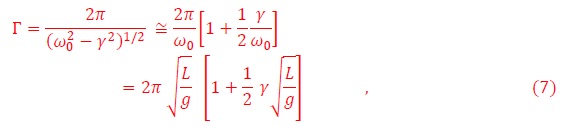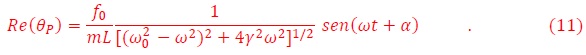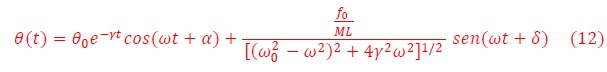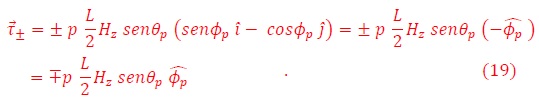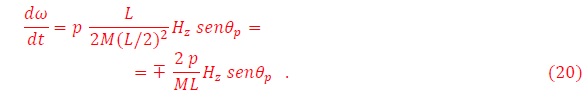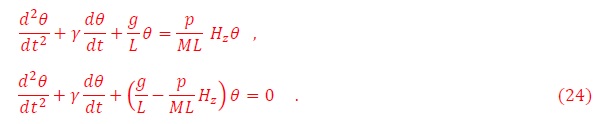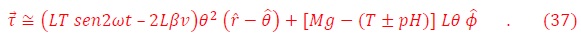El péndulo magnético
Hola de nuevo a todos, apreciados colegas y amigos de STEEMIT. De nuevo trayéndoles lo más destacado de mis archivos de Física Básica, en este caso el magnetismo. En Capítulos anteriores de la serie “La Física es Divertida” hemos estado discutiendo temas de nuestra vida donde el magnetismo es pilar fundamental. Entre estos hemos discutido temas tales como la rotación de La Tierra, las leyes de la magnetostática, polos magnéticos, la brújula, entre otros. Si se han perdido ésta Serie les invito a viajar por los enlaces:
https://steemit.com/stem-espanol/@jfermin70/misterios-magneticos
https://steemit.com/stem-espanol/@jfermin70/misterios-magneticos-2
Aunque parezca extraño, este Capítulo de “Misterios Magnéticos” está basado en una clase de mecánica dirigida a estudiantes de Ingeniería de la Universidad Rafael Urdaneta, en Maracaibo: “ondas mecánicas”. Aún cuando nos rodean los péndulos por todas partes, sorprendentemente pocos fueron capaces de describir un péndulo simple y dar ejemplos de la cotidianidad.
No hemos percibido que cuando sopla el viento, las hojas de un árbol y los cables colgando en los postes realizando movimientos de vaivén, tal como el péndulo. Un trapecista se impulsa como un péndulo para salir del trapecio. El corazón es una bomba mecánica que impulsa la sangre por nuestro cuerpo, en un movimiento de ida y vuelta como un péndulo. Los relojes mecánicos son péndulos.
El problema se complica cuando involucramos a los campos magnéticos. Estamos rodeados de campos magnéticos por todas partes. Es inevitable. La Tierra tiene un campo magnético de 0.5 Gauss, suficiente para orientar la aguja de una brújula, y guiar a las aves en su travesía a través del planeta. Los insectos también se orientan siguiendo el campo magnético terrestre. Ciertas bacterias se desarrollan o mueren dependiendo de la intensidad y frecuencia del campo magnético.
Ahora bien, los planetas giran alrededor del Sol tal como lo hace un péndulo alrededor de un punto fijo. Pero también giran alrededor de su propio eje, en movimiento de rotación. Un péndulo simple bajo la acción de la gravedad no rota. Entonces surgen algunas cuestiones,
…¿el movimiento pendular de los cuerpos celestes se debe únicamente a la fuerza gravitatoria?...
…¿existe algo más que la gravedad en el espacio, responsable de la dinámica de los cuerpos celestes?...
…¿qué ocurre cuando un péndulo se mueve en presencia de una fuerza diferente a la gravedad?...
…¿qué ocurre cuando esa fuerza adicional es magnética?...
Este trabajo es una combinación de mecánica clásica y electromagnetismo, cuyo objetivo es responder estas y otras cuestiones relacionadas con el péndulo. Para responder estas preguntas debemos observar y experimentar un poco. Les mostraré que podemos resolver problemas científicos de nuestro entorno sin equipamientos complejos y costosos, y sin tener gran experiencia en física. En este trabajo les propongo un paseo a través del movimiento de un péndulo magnético hecho en casa.
Con la finalidad de hacer este proyecto más interactivo, les agradezco dejarme sus inquietudes y preguntas en un REPLAY, y así darles respuesta.
Para más información sobre este tema y otros relacionados con Ciencia, Física y Tecnología, les invito visitar mis sitios:
luz.academia.edu/JoseFermin
www.researchgate.net/profile/Jose_Fermin
- El material presentado en este trabajo es original y propiedad del Autor
Física del péndulo
Desde el punto de vista coloquial o cotidiano, un péndulo es cualquier objeto que se mueve en un movimiento de vaivén. Formalmente, un péndulo es un cuerpo de masa m suspendida de un punto fijo, O, por medio de una cuerda de longitud L y masa despreciable, y que describe un movimiento oscilatorio alrededor de un eje que pasa por el punto O. En todos los cursos de Física básica se resuelve el problema del péndulo simple donde no hay fricción del medio. Sin embargo aquí nuestro péndulo oscila en un medio real con constante de viscosidad β, tal y como se muestra en la Figura 1,
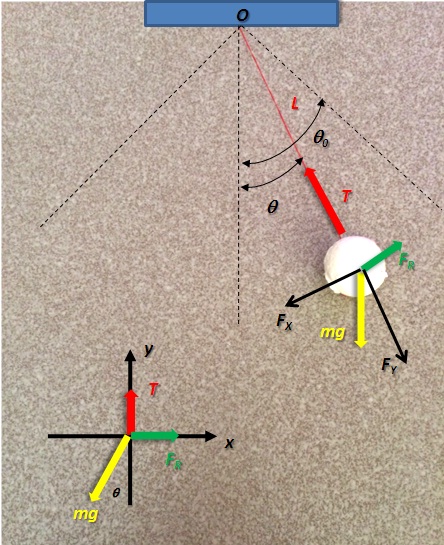
Figura 1. Péndulo simple amortiguado (Figura original propiedad del Autor)
Si el péndulo es llevado a una posición inicial θ0 este se moverá a lo largo de un arco de circunferencia s(t) = Rθ(t). Resolviendo el diagrama de fuerzas de la Figura 1, se obtiene la conocida ecuación del péndulo amortiguado,

donde γ= β/2mL es la constante de amortiguamiento y (g/L)-1/2 la frecuencia natural del péndulo. Esta es una ecuación no-lineal cuyas soluciones son integrales elípticas. Sin embargo, debido al amortiguamiento del medio, el ángulo de oscilación decaerá rápidamente y el péndulo ejecutará oscilaciones pequeñas. En ese caso θ∼0, y la ecuación 1 tendrá la forma más simple,

cuya solución general es,

θ0 y a son constantes que dependen de las condiciones iniciales. Esto corresponde a una oscilación de frecuencia angular ω12=ω02 - γ2 y amplitud θ0 exp(-γt). Estas oscilaciones tienen período,
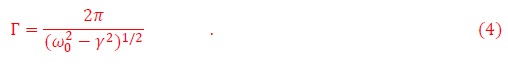
La viscosidad del medio incrementa el período de la oscilación. Si g=0, entonces el período corresponde al del péndulo simple,

En el régimen sub-amortiguado donde ω0 > γ, tenemos que el período del péndulo es,
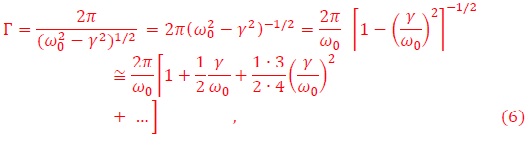
y en el caso de medios poco viscosos γ →0, tenemos que
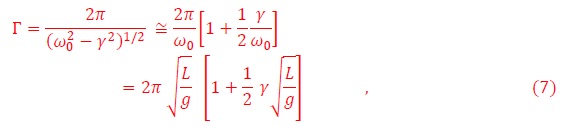

Si el péndulo oscila en presencia de una fuerza externa f(t), entonces la ecuación del movimiento es,

La solución de esta ecuación depende de la forma de la fuerza. En los cursos de Física básica universitarios se estudia el caso cuando la fuerza externa es periódica, es decir,

La solución particular es, en este caso dada por,

Cuya parte real es,
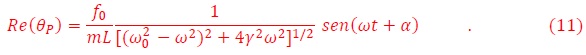
Finalmente, tenemos la solución general de (9),
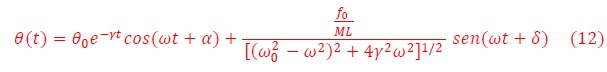
En la siguiente sección abordaremos el problema cuando la fuerza externa es producida por un imán.
El péndulo magnético
Antes de resolver el problema del péndulo magnético, es necesario revisar la dinámica de un dipolo magnético en un campo externo. Definimos un dipolo magnético, p, a un sistema formado por dos polos magnéticos (norte-sur) opuestos inherentes e inseparables: a) una barra magnetizada, b) un anillo metálico, c) cualquier material ferromagnético. El dipolo se orienta a lo largo de la línea imaginaria que une ambos polos, y a su vez genera un campo magnético en cualquier punto del espacio.
Este campo no es homogéneo sino más bien depende del punto de medición, es decir es inhomogéneo. Supongamos que colocamos una barra de hierro en el campo producido por un imán, como se muestra en la Figura 2.
https://cdn.steemitimages.com/DQmahgdvPEakTfLHjzfsGwvUzDYV9X9i3f6mSYiqYemqZXv/Figura%202.jpg)
Figura 2. Barra magnetizada en presencia de un campo magnético producido por un imán (Figura original propiedad del Autor)
La barra de hierro se magnetiza en presencia del campo magnético del imán, H, formando un dipolo magnético de intensidad p=m/L, donde m es el momento magnético. La fuerza magnética que actúa sobre la barra es,

Aquí (+/-) se refiere al polo (N/S) respectivamente. El centro de masa (CM) de la barra es atraído hacia el imán en un movimiento gobernado por las ecuaciones de movimiento,

donde

La solución de este sistema de ecuaciones involucra álgebras tediosas. Se nota sin embargo, la presencia de las derivadas temporales de θP y фP, es decir, existen torques inducidos por el campo sobre el dipolo. Entonces, en vez de resolver el sistema (15) utilizaremos la técnica del torque para analizar la dinámica del sistema. La fuerza (13) induce sobre la barra un torque magnético,

cuyas componentes son, en el caso general

En el caso más simple del campo magnético orientado a lo largo del eje “z” (Hx=Hy=0; H=Hz), el torque ejercido sobre la barra magnética está contenido en el plano (x, y) (ver Figura 2) y satisface la expresión,

o equivalentemente en coordenadas esféricas,
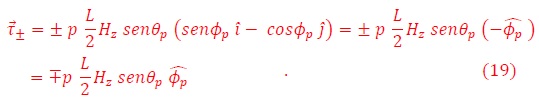
Este es un giro en el plano azimutal, es decir alrededor del eje “z”, adicionalmente a la traslación del centro de masa a lo largo de “z”. Utilizando las relaciones entre el torque y el momentum angular τ=dL/dt, y la expresión del momentum de un cuerpo rígido L=MR2ω, obtenemos la ecuación de la frecuencia del giro,
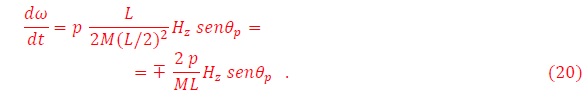
Integrando en un período de oscilación, Γ,

Mayor el campo, más rápido gira el objeto magnetizado. Con esto entonces hemos caracterizado el movimiento de una barra magnética en presencia de un campo externo. Lo mismo ocurre si en vez de una barra magnetizada colocamos una esfera magnetizada: rotará alrededor de su eje.
A continuación abordaremos el problema del péndulo magnético. Dos casos podemos analizar: a) imán estático; b) imán en movimiento periódico.
Campo estático.
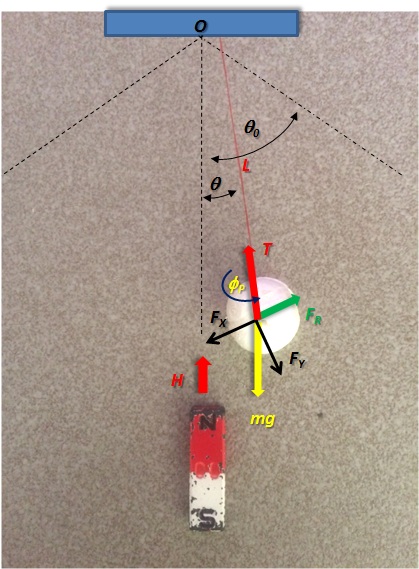
Consideremos ahora un péndulo magnético de masa M, oscilando en presencia del campo estático producido por un imán, como en la Figura 3. La masa está conectada a un punto fijo mediante una cuerda inelástica de masa despreciable y el campo en la dirección “z”.
Consideremos ahora un péndulo magnético de masa M, oscilando en presencia del campo estático producido por un imán, como en la Figura 3. La masa está conectada a un punto fijo mediante una cuerda inelástica de masa despreciable y el campo en la dirección “z”.
Figura 3. Péndulo magnético oscilando en presencia de un campo magnético estático (Figura propiedad del Autor).
El problema es similar al del objeto magnetizado, pero con la traslación del CM a lo largo del arco de circunferencia Lθ. Resolviendo el diagrama de fuerzas de la Figura 3 en el régimen de oscilaciones pequeñas se obtiene la ecuación simplificada para el CM,
A diferencia del péndulo simple, el periodo del péndulo magnético depende de la masa. Ahora bien, las ecuaciones (18) y (19) predicen que el campo magnético ejerce un torque que induce una rotación del objeto magnetizado alrededor de su propio eje. Entonces tenemos la ecuación del torque,
Nuestro análisis es muy simple y no se aplica al caso más general, pero nos permite representar razonablemente la dinámica de un péndulo magnético.
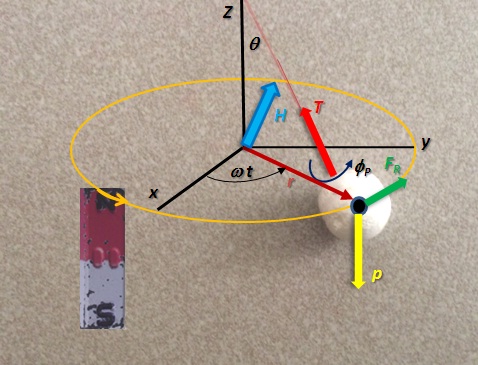
Consideremos ahora que el campo es producido por un imán que se mueve lentamente en un movimiento circular de frecuencia constante, ω, como en el esquema de la Figura 4.
Figura 4. Péndulo magnético en presencia de un campo variable. (Figura propiedad del Autor)
El sistema de referencia más conveniente tiene centro de referencia en el centro de la trayectoria ubicada en el plano horizontal (x, y), y eje “z” en la vertical. La trayectoria del péndulo es,