¡Hola amigos de Steemit!
Reciban un cordial saludo.
Desde nuestros inicios en la física y distintas áreas de la ingeniería nos encontramos con cantidades físicas en las que basta un numero para su cuantificación y descripción, a las que llamamos escalares. Por otro lado, también nos encontramos con cantidades físicas que requieren, además de un valor numérico que las cuantifique, una dirección y sentido que permita describir en su totalidad la información que aporta dicha cantidad, por lo que son conocidas como cantidades vectoriales.
La fuerza es uno de esos parámetros de carácter vectorial con el que debemos enfrentarnos en la descripción del comportamiento de un sin fin de sistemas físicos, ya sea de tipo mecánico, eléctrico o magnético.
En esta entrega compartiré con ustedes, de manera sencilla, un pequeño análisis teórico y experimental sobre el carácter vectorial de la fuerza, estudiaremos el equilibrio y la aceleración de un sistema, según lo establecen las leyes de Newton, cuando sobre el mismo actúan un conjunto de fuerzas.
----
Fundamentos teóricos
----
En la siguiente imagen se ilustra la acción de un conjunto de fuerzas que actúan sobre un objeto puntual, conocidas como fuerzas concurrentes.
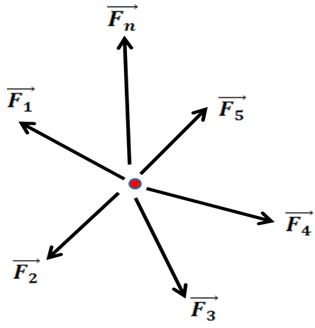
Figura 1 - Fuerzas concurrentes
(Elaborada por @lorenzor en PowerPoint)
En condiciones de equilibrio traslacional según lo establece la primera ley de Newton se debe cumplir que:
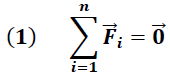
Donde “n” representa el número de fuerzas actuantes.
La Ecuación (1) es usualmente expresada para mayor facilidad en coordenadas cartesianas de la forma:
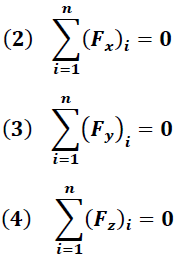
Estas expresiones bajo la condición de fuerzas concurrentes, son suficientes para garantizar el equilibrio traslacional del sistema.
En un sistema que no se encuentre en equilibrio traslacional, la ecuación (1) pierde validez y debe ser generalizada según lo expresa la segunda Ley de Newton a la forma:
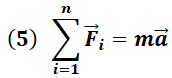
En este caso la masa “m” sobre la que actúan las fuerzas se encuentra acelerada debido a que la resultante del conjunto de fuerzas aplicadas no es nula.
La ecuación (5), al igual que la ecuación (1), es expresada para cada uno de los ejes coordenados por medio de las siguientes expresiones:
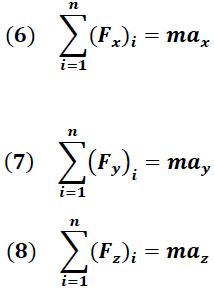
De las ecuaciones anteriores parten muchos de nuestros análisis al momento de solucionar una gran variedad de problemas físicos.
A continuación, se muestra un pequeño desarrollo experimental que permite consolidar el carácter vectorial de la fuerza y afianzar la validez de las leyes de Newton en las que se sustentan las condiciones de equilibrio y sistemas acelerados.
----
Parte experimental
----
Instrumentos y materiales utilizados

Figura 2 - Instrumentos y materiales utilizados en el laboratorio
(Fotografía tomada en el laboratorio por @lorenzor)
Parte experimental 1 (Equilibrio)
Para nuestro primer ensayo sobre un sistema en equilibrio utilizaremos una tabla de fuerzas de laboratorio como se muestra en la figura 3 donde las fuerzas que actúan son de tipo concurrentes (coplanares).
El procedimiento a seguir consiste en la aplicación de un conjunto de fuerzas sobre el aro central, el cual generara una fuerza resultante hacia donde el aro tendera a desplazarse.
Las fuerzas son ejercidas por masas cuyos pesos determinaran su valor en las direcciones indicadas.
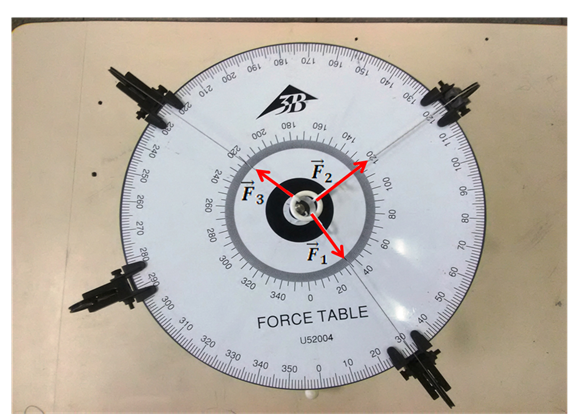
Figura 3 - Fuerzas aplicadas en la tabla de prueba
(Fotografía tomada en el laboratorio por @lorenzor y editada en Powerpoint)
Esta fuerza resultante puede ser equilibrada con una fuerza contraria conocida como fuerza equilibrante https://cdn.steemitimages.com/DQmTuW4H7ara5P4UcHfi3s5b5LDC9pkrRbDwB2Yab9UVA5X/image.png, la cual obliga al aro a centrarse debido a el equilibrio obtenido.
Existen varios métodos para la obtención de la fuerza resultante. El método que aplicaremos en este primer análisis consistirá en la representación vectorial de cada una las fuerzas actuantes a través de sus componentes rectangulares.
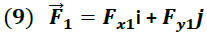
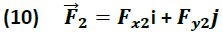
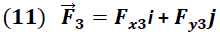
Donde 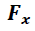 y 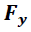 representan las componentes horizontal y vertical de los vectores fuerza respectivamente y son obtenidas a través de las ecuaciones.
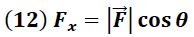
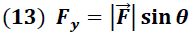
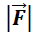 → Magnitud del vector Fuerza
θ → ángulo del vector fuerza respecto al eje + x
La fuerza resultante sobre el aro está dada por la suma de todas las fuerzas según la siguiente expresión:
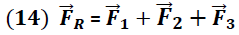
La fuerza requerida para centrar el anillo o aro debe ser de igual magnitud y en dirección contraria a la fuerza total:
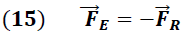
----
Cálculos y resultados
----
Fuerzas y direcciones utilizadas
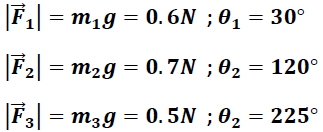
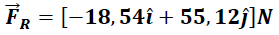
En magnitud:
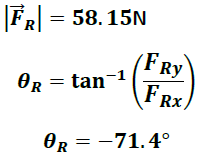
Los resultados obtenidos ubican la fuerza resultante en el segundo cuadrante del plano. De modo que la fuerza requerida para el equilibrio está ubicada a 180 ͦ según se muestra en la siguiente imagen.

Figura 4 - Representación gráfica de la fuerza equilibrante en la tabla de prueba
(Fotografía tomada en el laboratorio por @lorenzor y editada en PowerPoint)
En la Figura 4 se observa que, dada las propiedades vectoriales de la fuerza, es posible determinar con exactitud la dirección y magnitud de la fuerza requerida para el equilibrio lo cual, además, obedece a lo postulado por la condición de equilibrio traslacional establecido por la ecuación 1.
Parte experimental 2 (Sistema Acelerado)
En la siguiente sección analizaremos, teórica y experimentalmente, la aceleración de un sistema debido a la acción de las fuerzas actuantes y, además, demostraremos la validez y aplicación de las Leyes de Newton en la solución de estos sistemas.
En la siguiente imagen, tomada en el laboratorio, se muestra el montaje experimental de un sistema para la obtención de la aceleración de las masas que lo constituyen.
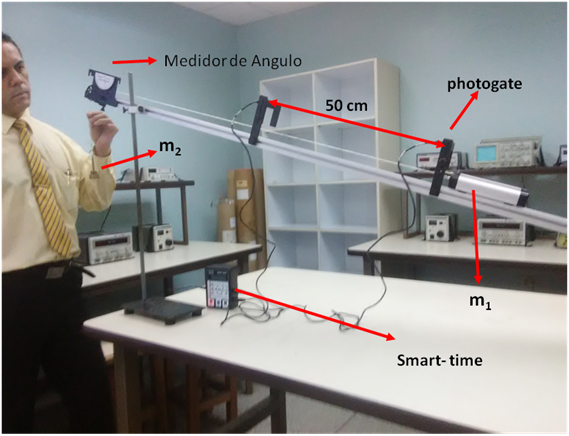
Figura 5 - Montaje del Sistema acelerado
(Fotografía tomada en el laboratorio por @lorenzor y editada con PowerPoint)
En el sistema la masa “m2” sujeta a la masa “m1” a través de una cuerda se dejara caer (V0=0) provocando que ambas masas se aceleren.
Las fotoceldas (photogate) conectadas al equipo (Smart- time), en su modo de medidor de tiempo, permiten conocer con alta precisión el tiempo de transito de la masa “m1” para la distancia seleccionada entre ellos y el posterior cálculo de la aceleración que esta experimenta.
Valores obtenidos
Tiempo promedio de transito de la masa “m
1” entre las dos fotoceldas.
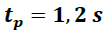
Distancia entre las fotoceldas:
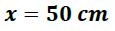
----
Cálculos y resultados
----
De acuerdo a las formulas básicas de cinemática tenemos que:
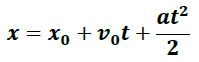
Si x0 = 0 y v0 = 0
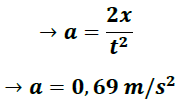
Este resultado puede ser obtenido, a partir de las Leyes de Newton, realizando un análisis de las fuerzas que actúan en el sistema tal y como se muestra a continuación. (Ver figura 6)
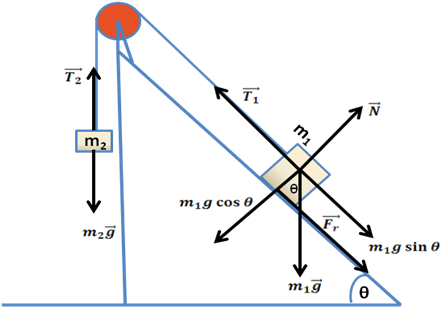
Figura 6 - Diagramas de fuerzas actuantes sobre las masas constituyentes del sistema
(Elaborada por @lorenzor en PowerPoint)
Para simplificar nuestro análisis, consideraremos que no existen fuerzas de roce significativas entre cuerda - polea y entre masa m1 - superficie.
Fr = 0 ( Fuerza de roce)
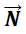 → Fuerza de reacción (Normal)
θ → ángulo de inclinación del plano
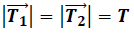 (Tensión en la cuerda de masa despreciable)
De las leyes de Newton obtenemos, en la dirección del movimiento, el siguiente sistema de ecuaciones:
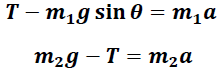
La solución de este sistema nos conduce a la siguiente expresión de la aceleración:
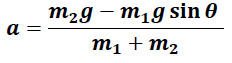
De los valores obtenidos en el laboratorio m1 = 490 gr ; m2 = 170 gr ; θ = 15° se obtiene:
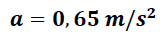
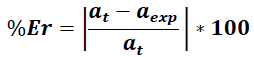
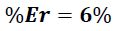
El resultado obtenido permite validar las leyes de Newton y la metodología aplicada en la determinación de la aceleración de un sistema.
Las condiciones de equilibrio y sistemas acelerados que se han estudiado en este trabajo, fundamentadas en las Leyes de Newton, constituyen uno de los pilares más importantes de la física clásica. Estos principios son ampliamente utilizados en el estudio de la dinámica o equilibrio de sistemas, desde los más simples hasta lo más complejos. La finalidad de este trabajo ha sido afianzar y fortalecer nuestros conocimientos y las aplicaciones de las leyes fundamentales que rigen el equilibrio y el movimiento de los cuerpos.
Si tienen alguna pregunta, duda o sugerencia, dejen sus comentario y con mucho gusto les responderé.
Gracias por leer mi publicación.
----
Referencias
----
* Física para Ciencias e Ingeniería. Fishbane, Gasiorowicz, Thornton. Volumen I. Prentice Hall.
* Física para la Ciencia y la Tecnología. Tipler Mosca. Volumen 1: Mecánica. Oscilaciones y ondas. Termodinámica. 5a edición. Editorial Reverté.
* Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo I. McGraw-Hill.
* Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 1. Addison Wesley Longman.