¡Hola amigos de Steemit!
Reciban un cordial saludo.
En este artículo compartiré con ustedes un pequeño análisis teórico y experimental de uno de los movimientos con el que iniciamos nuestro aprendizaje en la física y distintas aéreas de la ingeniería.
El movimiento parabólico
Este movimiento ha sido atribuido casi con exclusividad al movimiento de un proyectil. Sin embargo, existen una gran cantidad de casos donde la compresión y aplicación de este movimiento ha facilitado de manera importante el análisis de fenómenos físicos donde dicho movimiento está presente.
De la misma forma que una partícula de masa “m” se ve afectada por un campo gravitatorio que la obliga a describir este movimiento parabólico, una partícula cargada describe este mismo movimiento cuando entra en un campo eléctrico uniforme, tal y como se observa en las partículas cargadas que se mueven entre las placas deflectoras de un tubo de rayos catódicos.
Con el objeto de afianzar y fortalecer nuestros conocimientos en este tipo de movimiento, haremos una revisión teórica y algunos ensayos experimentales realizados con instrumentos tradicionales y equipos de alta precisión que en la actualidad facilitan el estudio de dicho movimiento.
----
Fundamentos teóricos
----
Para facilitar nuestro análisis experimental, definiremos a continuación las ecuaciones de movimiento de una partícula que se mueve bajo la acción de un campo gravitatorio. En la figura 1 se ilustra un ejemplo del camino que sigue una partícula en el campo gravitatorio cuando es lanzada con una velocidad inicial VO y un ángulo θ.
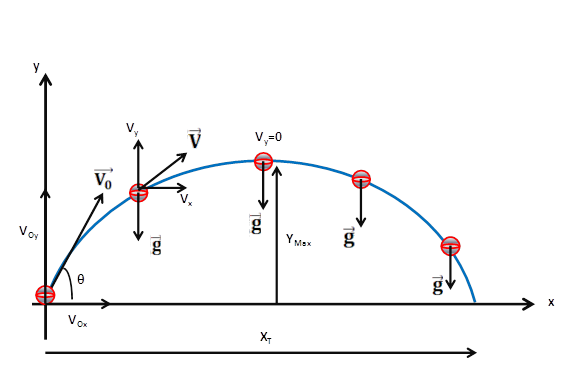
Figura 1 – Movimiento parabólico de una partícula
(Elaborado por @lorenzor)
Las ecuaciones asociadas a este movimiento son obtenidas a partir de la segunda ley de Newton de manera independiente para el caso horizontal y vertical como se muestra a continuación:
Movimiento horizontal
Aplicando:
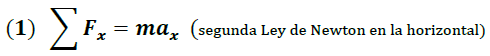
Dado que en la horizontal no actúan fuerzas 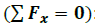:
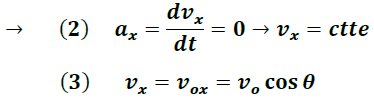
Por definición se tiene:
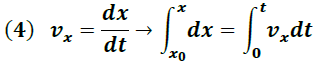
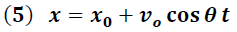
Movimiento vertical

Para el caso vertical la única fuerza que actúa sobre la partícula, despreciando la resistencia del aire, es la ejercida por su peso 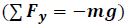 .
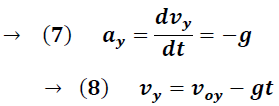
Donde:
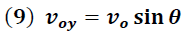
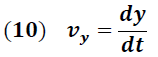
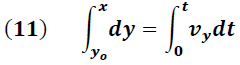
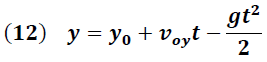
La ecuación (12) es regularmente escrita en función de la variable x y el ángulo θ. Para esto debemos reemplazar (5) y (9) en (12), obteniéndose la siguiente ecuación:
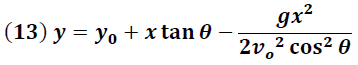
---
Parte experimental
---
Instrumentos y Materiales utilizados

Figura 2 – Instrumentos y Materiales utilizados en los ensayos
(Fotografía tomada en el laboratorio por @lorenzor)
Experimento 1
En nuestro primer ensayo experimental, visualizado en la siguiente imagen tomada en el laboratorio, una esfera metálica de masa “m” es soltada desde el punto A que se identifica en la figura 3.
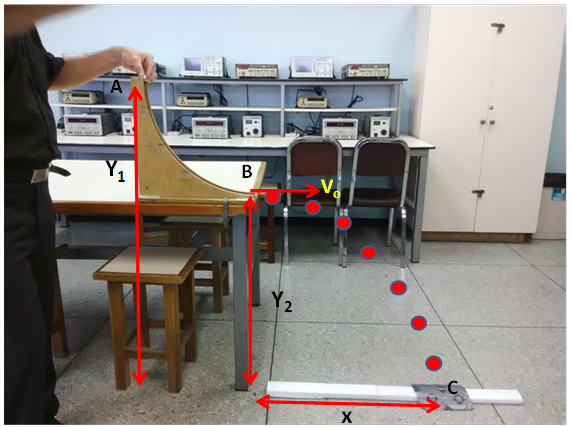
Figura 3 – Primer ensayo experimental del movimiento parabolico
(Fotografía tomada por @lorenzor y editada en Powerpoint)
La esfera se desliza a través de la curva y es disparada horizontalmente (θ=0) en su salida en el punto identificado como B. El movimiento que esta sigue desde el punto B hasta el punto de impacto el cual es identificado como C, es un movimiento parabólico bajo la acción del campo gravitatorio en el que las ecuaciones definidas en nuestro fundamento teórico son aplicables.
Nuestro objetivo en este ensayo consiste en determinar, usando las ecuaciones de movimiento, la velocidad de la partícula en el punto B, la cual corresponde a la velocidad inicial del movimiento parabólico. Como podemos observar este valor de velocidad será determinado con datos fácilmente obtenidos con instrumental básico.
Los registros de los impactos son mostrados en el riel colocado en el suelo los cuales son identificados usando papel carbón que permite promediar las muestras obtenidas.
Valores obtenidos de las mediciones

Distancia horizontal promedio 𝒙=𝟗𝟓 𝒄𝒎
Cálculos y resultados
La aplicación de la ecuación (13) ajustada a las condiciones impuestas por el experimento realizado se simplifica a la forma:
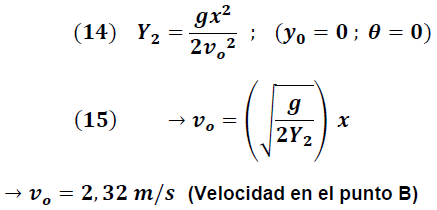
Una forma de verificar el resultado obtenido es la determinación de la velocidad final de la partícula en el tramo AB a partir de un análisis de energía.
Si consideramos que la fuerzas disipativas o de fricción son pequeñas o despreciables, el principio de conservación establece:
Energía mecánica total en A = Energía mecánica total en B
Debe notar que la energía atribuida a la partícula en el punto A es de tipo potencial, mientras que la energía en el punto B es compartida entre cinética y potencial.
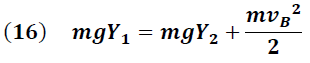
De lo cual obtenemos que:
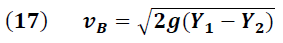
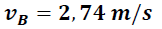
De esta forma podemos apreciar que la velocidad obtenida a partir de consideraciones energéticas muestra una coincidencia cercana al valor de velocidad obtenido en el movimiento parabólico, validando el método y el instrumental utilizado en este primer ensayo.
Experimento 2
En esta sección haremos uso de instrumental PASCO de alta precisión para la obtención de datos del movimiento parabólico.
En la siguiente imagen tomada en el laboratorio se observa la metodología experimental utilizada para determinar la velocidad inicial de la partícula.
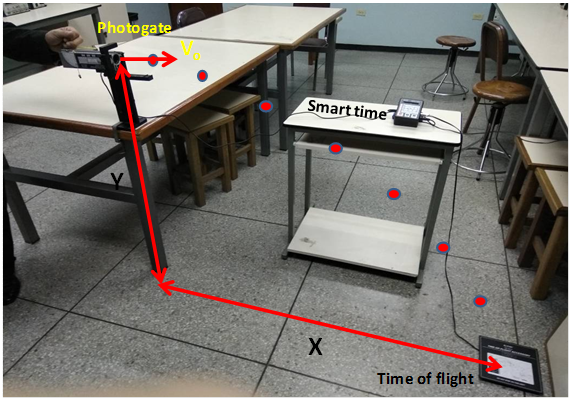
Figura 4 – Movimiento parabólico con instrumental PASCO
(Fotografía tomada por @lorenzor y editada en Powerpoint)
En este ensayo la partícula es disparada por el lanzador (projectile launcer) donde un sensor (Photogate) conectado al medidor de tiempo (Smart- time) y colocado en la boca del equipo detecta su salida a través de un infrarrojo, activando el reloj, el cual es detenido una vez que la esfera impacta sobre la tabla en el suelo (sensor de tiempo total).
Valores obtenidos de las mediciones
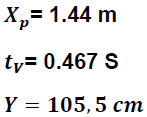
Cálculos y resultados
De la ecuación (12) para un lanzamiento con (θ=0) tenemos:
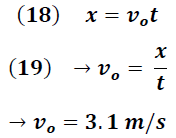
La velocidad obtenida puede ser verificada colocando un segundo sensor de luz de la forma que se muestra en la siguiente imagen:

Figura 5 – Ensayo experimental para la determinación inicial de la partícula con el método del doble sensor (Photogate)
(Fotografía tomada por @lorenzor y editada en Powerpoint)
En este caso el segundo sensor conectado al Smart-time permite registrar el tiempo que tarda la partícula en recorrer 10 cm. La velocidad obtenida por este método arroja un valor de 3.03 m/s, lo cual coincide con alta precisión con el valor obtenido a partir de las ecuaciones de movimiento, evidenciando que el instrumental utilizado ofrece menores márgenes de error en el proceso experimental.
Experimento 3
Otro ensayo de importancia en el estudio del movimiento parabólico es la determinación del valor de la aceleración de la gravedad a partir de los valores de la posición horizontal (x) versus los datos obtenidos de la posición vertical (Y) de la partícula.
La ecuación (13) simplificada para un lanzamiento horizontal (θ=0) es la expresión que nos permite alcanzar este objetivo.
En una representación grafica de las posiciones verticales versus los valores cuadráticos de las posiciones horizontales, la pendiente de la recta “m” obtenida es una función de la velocidad de la partícula y de la aceleración de la gravedad tal y como se observa en la ecuación (20):
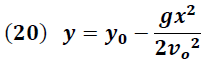
De tal forma que la determinación de esta pendiente es la clave para la obtención de la gravedad tal y como se expresa en la siguiente ecuación:
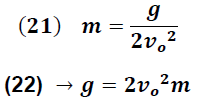
Para este fin se procede como se muestra en la imagen 6 que se muestra a continuación:

Figura 6 –Obtención experimental de las coordenadas X vs Y.
(Fotografía tomada por @lorenzor)
En este caso los datos son obtenidos desplazando en la horizontal la tablilla en la que se registran para cada posición “x” los puntos de impacto de que corresponden a la posición vertical (Y) de la partícula.
Este proceso es repetido para cada posición de “x” el número de veces que el experimentador considere oportuno.
En la siguiente tabla se muestra los valores promedios de las posiciones verticales (YP) obtenidos para cada valor de “x” seleccionado.
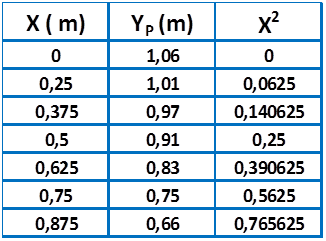
Tabla de valores obtenido X y X2 versus Y.
(Tabla elaborada por @lorenzor en Microsoft Excel)
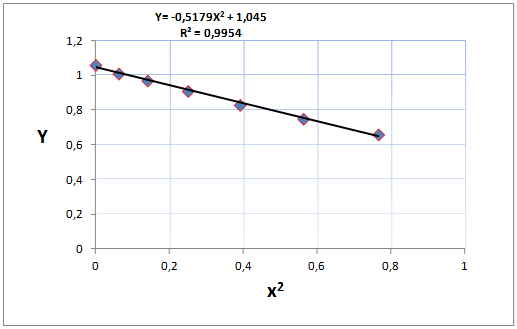
Figura 7. Representación grafica de los valores verticales versus los valores cuadráticos de posición horizontal.
(Elaborada por @lorenzor en Microsoft Excel)
En la ecuación de la línea recta que se muestra dada por:
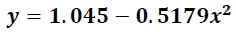
Se tiene que la magnitud de la pendiente es:
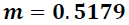
Nos conduce según la expresión (22) al valor de la gravedad:
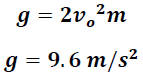
El valor obtenido de la gravedad a través de este método es cercano al valor teórico aceptado de 9,81 m/s2.
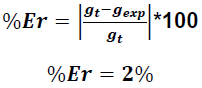
De esta forma podemos apreciar que las distintas metodologías experimentales utilizadas en este artículo permiten el análisis y validación de los conceptos físicos y fundamentos teóricos inherentes a uno de los movimientos que experimentan en la naturaleza distintos objetos o partículas.
Espero que el desarrollo teórico y experimental expuesto en este trabajo permita fortalecer sus conocimientos sobre uno de los movimientos que está presente en una gran variedad de fenómenos físicos. Si tienen alguna pregunta, duda o sugerencia, dejen sus comentario y con mucho gusto les responderé.
Gracias por leer mi publicación.
----
Referencias
----
* Física para Ciencias e Ingeniería. Fishbane, Gasiorowicz, Thornton. Volumen I. Prentice Hall.
* Física para la Ciencia y la Tecnología. Tipler Mosca. Volumen 1: Mecánica. Oscilaciones y ondas. Termodinámica. 5a edición. Editorial Reverté.
* Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo I. McGraw-Hill.
* Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 1. Addison Wesley Longman.