
https://steemitimages.com/DQmPfwR6jw8Ac8EaqZceTQQgyrjwZsDyeCTbBDVH8A6hY3b/descarga.jpg
La evolución es producida como resultado de la selección natural y la reproducción sexual. Charles Darwin publicó en 1859 su libro “El origen de las especies” el cual causó numerosas polémicas en el mundo de la ciencia por las teorías que sostenían que las especies evolucionan de acuerdo al medio ambiente para poder adaptarse a él. Fue una discusión entre los que pensaban que el mundo era una creación estática y perfecta de dios contra teorías sobre como los individuos se encontraban en constante competencia y evolución para poder perpetuar su especie a través del tiempo. Las especies se crean, evolucionan y desparecen si no se logran adaptar, de modo que solo los más aptos, es decir, los que mejor se adapten al medio ambiente sobreviven y logran perpetuar sus aptitudes.
De acuerdo a este punto de vista de la evolución, la computación ve en dicho marco un proceso claro de optimización: Se toman los individuos que se han adaptado mejor, las mejores soluciones temporales, se cruzan y/o mezclan generando nuevos individuos o nuevas soluciones que contendrán parte del código genético o información de sus antecesores, y el promedio de adaptación de toda la población se mejora.
La computación evolutiva (CE) se ha convertido en un concepto general que se adapta para la resolución de problemas, específicamente para problemas de optimización, debido a que añade flexibilidad y adaptabilidad en la resolución, combinables con la robustez y las ventajas de la búsqueda global.
¿Qué es la Computación Evolutiva?
https://steemitimages.com/DQmddWrCPAAkSjd6CdAXQgYcmaQM7eTF9bmXSKLD4d4dGBo/CE1_Jarroba.com_.png
La computación evolutiva (CE) es una rama de la inteligencia artificial que se enfoca en las técnicas que simulan la evolución natural, y constituye un enfoque alternativo para tocar problemas complejos de búsqueda y aprendizaje a través de modelos computacionales de procesos evolutivos e involucra problemas de optimización combinatoria. La CE estaba basada en los mecanismos de evolución biológica que fueron propuestos por Darwin, Lamark y Medel; siendo Darwin quien propuso la "Selección natural de los más adaptados", Medel propuso la "Teoría corpuscular de la herencia" y Lamark propuso la "Herencia de caracteres adquiridos".
La CE trata de resolver problemas de optimización combinatoria con el fin de poder encontrar la mejor solución a un problema, es decir, al igual que en la naturaleza sólo los más fuertes y mejores adaptados al ambiente son capaces de poder sobrevivir, reproducirse y perpetuar su especie a través del tiempo.
La CE engloba diferentes estrategias para la resolución de los problemas de optimización, las cuales son:
Procesos de búsqueda evolutiva: Esta fue propuesta por Alan Turing en el año 1948.
Estrategias Evolutivas: Esta representa los individuos a través de vectores reales. Fue propuesta por Rechenberg en el año 1964
Programación Evolutiva: Esta utiliza máquinas de estado finito. Fue propuesta por Fogel en el año 1965.
Algoritmos Genéticos: Esta representa a los individuos como cadenas binarias y fue propuesta por Holland en el año 1975.
Programación Genética: Utiliza arboles LISP y fue propuesta por Koza en 1992.

Algoritmos Evolutivos
Este término se emplea para describir sistema de resolución de problemas de optimización o búsquedas que se basan en un ordenador y se emplean modelos computacionales de algún mecanismo de evolución conocido como elemento clave en su diseño y en su implementación.
Los algoritmos evolutivos toman como inspiración la evolución en diferentes sistemas biológicos y su idea principal es mantener un conjunto de individuos los cuales representan una posible solución a un problema. Los individuos se mezclan y compiten entre ellos mismos en donde solo los que mejor se adapten serán los que sobrevivirán. Como pueden notar estos algoritmos imitan el principio de “selección natural” que fue propuesto por Charles Darwin.
Componentes principales:
Población de individuos, que son una representación de posibles soluciones.
Procedimiento de selección basado en la aptitud de los individuos para resolver el problema.
Procedimiento de transformación para construir nuevos individuos a partir de los anteriores.
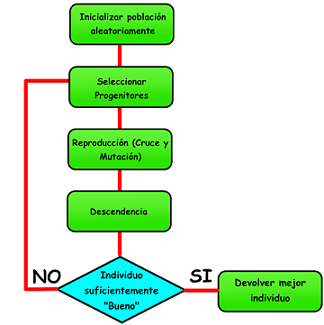
Esquema General de un Algoritmo Evolutivo
BEGIN
INICIALIZAR de forma aleatoria una población con soluciones candidatas EVALUAR cada candidato
REPEAT UNTIL ( CONDICIÓN DE TERMINACIÓN == true )
1. SELECCIONAR progenitores
2. RECOMBINAR progenitores seleccionados obteniendo descendencia
3. MUTAR descendencia
4. EVALUAR nuevos candidatos
5. SELECCIONAR individuos para la próxima generación
END REPEAT
END
Pseudo-código de algoritmo evolutivo
Características:
Estrategias Evolutivas: Desarrollada por Rechenberg y Schwefel y extendida por Herdy, Kursawe, Ostermeier, Rudolph, y otros, fue diseñada con el propósito de resolver problemas de optimización discretos y continuos. Trabaja con vectores de números reales que codifican las posibles soluciones de problemas numéricos. Este utiliza recombinación o cruce (crossover aritmético), mutación y la operación de selección, pudiendo ser determinística o probabilística, elimina las peores soluciones de la población y no genera copia de aquellos individuos con una aptitud por debajo de la aptitud promedio.
Programación Evolutiva: Fue introducida por Fogel y extendida por Burguin, al principio fue diseñada con el propósito de crear inteligencia artificial. La representación del problema se hace mediante números reales y emplea mecanismos de mutación y selección.
Algoritmos Genéticos: Trabajan con cadenas binarias para la representación del problema y el espacio de las soluciones que son posibles es explorado aplicando transformaciones a éstas soluciones candidatas así como podemos observarlo en los organismos vivos: cruce, inversión y mutación.
Programación Genética: Fue desarrollada por Koza, los individuos son programas o autómatas de longitud variable, están descritos a través Expresiones-S de LISP y se representan como árboles, y como operadores de variación emplea crossover y modificación, además de mecanismos de selección.
¿Cómo se representan los individuos?
Podemos decir que cada persona posee una información genética única la cual se encuentra en el ADN. El ADN está compuesto por cuatro tipos de elementos: la "Adenina" (A), "Timina" (T), "Citosina" (C) y "Guanina" (G), podemos decir que los seres humanos estamos representados por medio de un ARRAY (Arreglo) compuesto por alguno de estos 4 "elementos" y con esto tenemos una manera de representar los individuos. Pasando esto a un problema de optimización combinatoria, quiere decir que un posible resultado al problema lo podemos pasar a un array que podría estar lleno de ceros o unos (binario), al que le daremos un cierto significado y a este array que representa al individuo se le denomina Cromosoma.
https://steemitimages.com/DQmTbCzBMS14Ybiuh424BNGSXpYsxjdb9Tc4P3jhmQfwzpu/image14.png
¿Cómo se representan los individuos?
Podemos definir el proceso de reproducción como la creación de un nuevo individuo a partir de dos individuos dados, es decir, haciendo una combinación de dos arrays que representan a dos individuos. Aquí les dejo un ejemplo de como sería este proceso
:
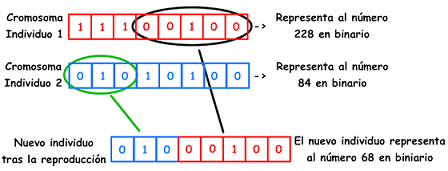
Así es como funciona la reproducción humana, pues al nacer el individuo hereda unas características de la madre y otras del padre. No se tiene porque heredar en partes iguales las características de los dos progenitores.
En referencia a la generación de nuevo individuos, existe la posibilidad de que ocurra una mutación en algún gen; es decir, que sin ninguna "lógica" un elemento específico del cromosoma cambie su valor, por ejemplo:

Algoritmos Genéticos
Los algoritmos genéticos trabajan sobre un conjunto de soluciones potenciales, la cual se denomina población. Esta población está compuesta por una serie de soluciones que se le llaman individuos y un individuo está conformado por una serie de posiciones que representan cada una de las variables involucradas en los procesos de optimización llamados cromosomas. Los cromosomas están compuestos por una cadena de símbolos que en la mayoría de los casos es representada en números binarios. En un algoritmo genético cada individuo está definido como una estructura de datos que representa una posible solución del espacio de búsqueda del problema. Las estrategias de evolución trabajan sobre los individuos, los cuales evolucionan a través de generaciones. Dentro de la población cada uno de los individuos es diferenciado por su valor de aptitud, el cual obtienen usando algunas medidas de acuerdo con el problema que se va a resolver. Para la obtener las próximas generaciones se crean nuevos individuos, los cuales son llamados hijos, utilizando dos estrategias de evolución básicas como son el operador de cruce y el de mutación las cuales se emplean generalmente de una manera aleatoria.

Fuente de las Imágenes:
A B C D E F G H
Referencias Bibliográficas:
Libro: Inteligencia Artificial un enfoque moderno, segunda edición. Stuart J. Russell & Peter Norvig.
Espero que les haya gustado el post, muchas gracias por sus comentarios y haberme leído,hasta la próxima.
https://steemitimages.com/DQmPdCKiQC6RHzRt4EfvjihVwF1UUya1U3tdRf25o3HzaAq/giphy.gif