Importancia y aplicaciones de la Computación gráfica

Otras aplicaciones de la Computación gráfica:

1. Interfaces con el usuario.
2. Graficación interactiva en los negocios, tecnología y ciencia.
3. Cartografía (mapas, relieves, ríos).
4. Medicina.
5. Bosquejos y diseños asistidos por computadoras, Ejemplo: AutoCAD.
6. Sistemas Multimedia (conferencias, videoteléfono, docencia a distancia).
7. Simulación para entrenamiento civil y militar.
8. Animación de personajes para el cine y la televisión.

Algoritmos Básicos de Gráficos Bidimensionales

1. Discretización de líneas

• A partir de la ecuación de la recta, podemos calcular puntos entre los extremos de una línea y dibujarlos en pantalla.
• Dado un segmento según sus extremos (x₁, y₁) y (x₂, y₂), la ecuación de la recta que los une puede escribirse como:


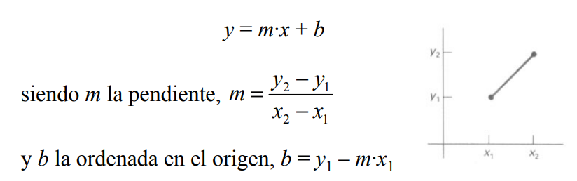
• Suponiendo que disponemos de una cierta función putPixel(...) que nos permite colorear un pixel en pantalla, el código en C de este primer algoritmo podría ser el siguiente:


• Un primer defecto de este código es que sólo es válido si la coordenada x del primer extremo de la línea es menor que la del segundo extremo.
• Pendientes y orden de los extremos.
  • Muchos algoritmos toman como hipótesis que el segmento se encuentra en el primer cuadrante.

• Otro defecto más del código anterior es que sólo funciona bien con pendientes pequeñas, pues con líneas de pendientes más altas deja huecos indeseables.
• Pero el principal problema es el empleo de aritmética en coma flotante, en especial la multiplicación del bucle interior, muy costoso en tiempo de CPU.

2. Analizador diferencial digital (DDA)

• Algoritmo Incremental Básico:
  • Es posible eliminar la multiplicación dentro del bucle si observamos que:



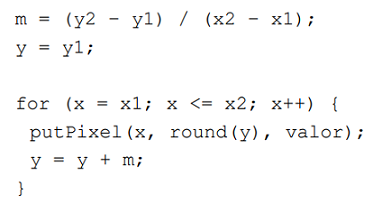
Ejemplos:

• Dibujar una línea desde (1,1) hasta (6,3):

 

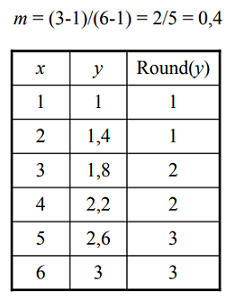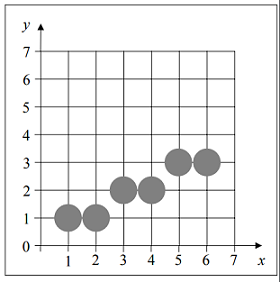
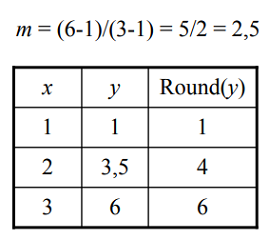
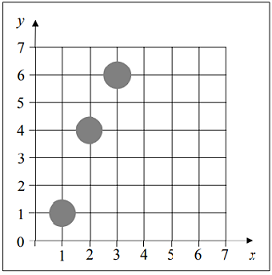
• Dibujar una línea desde (1,1) hasta (3,6):

 

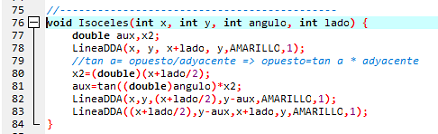
• En este ejemplo les mostraré la figura de un triangulo isósceles hecho mediante las lineas DDA realizado en lenguaje C mediante el DevC++.



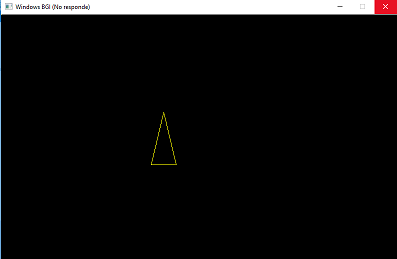
Fuente Propia


3. Discretización de Circunferencias

• Ecuación de una circunferencia centrada en el origen: x² + y² = R²
• Ecuación explícita de la circunferencia: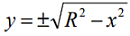 

  • Es posible dibujar un cuarto de circunferencia incrementando x de 0 a R en pasos unitarios (los otros cuartos se obtienen por simetría), pero aparecen grandes huecos al acercarnos a R.
• Ecuaciones Paramétricas: x = R·cos θ y = R·sen θ
  • Evitamos los huecos aumentando el ángulo θ de 0º a 90º.

-Simetría de ocho lados:

• Dado una circunferencia centrada en el origen y un punto sobre ella, podemos fácilmente obtener siete puntos adicionales a ése.


-Algoritmo del punto medio.

• Consideramos sólo 45º de la circunferencia, el segundo octante, de x = 0 a x = y = R / √2.
• Usaremos la función puntos_círculo(...) para completar el resto de la circunferencia.
• La estrategia consiste en seleccionar cuál de dos pixels está más cercano a la circunferencia, evaluando la función en el punto medio entre dos pixels.
• En el segundo octante, la siguiente elección de pixel es entre el pixel E y el pixel SE, y se basará de nuevo en una variable de decisión d:



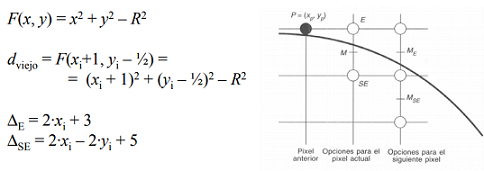
Ejemplo:


Fuente Propia

Ahora voy a mostrarle un pequeño dibujo en el cual utilizo un algoritmo para realizar relleno, las lineas DDA y el de las circunferencias:


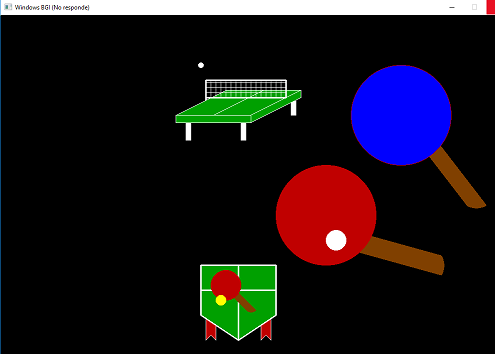
Fuente Propia

Este dibujo utiliza un algoritmo de relleno, el cual consiste en que se le pasa por parámetro las coordenadas (x,y) en donde se empezara a pintar, luego se envía el color que pintará y por ultimo el color del borde de la figura el cual será el punto donde terminará de pintar. Fue realizado en DevC++


Fuente de las Imágenes: A B C 

Referencias Bibliográficas:

1. Sitio Web: http://graficacionheribertojesus.blogspot.com/p/61-instalar-evaluar-los-principales.html
2. Libro: Una Humilde Introducción a la Graficación por Computadora y Otras Yerbas. Eduardo Navas

Espero que hayan disfrutado este contenido, hasta la próxima.