Mit dem Epsilon Delta Kriterium wird die Stetigkeit einer Funktion f bewiesen.
Stetigkeit bedeutet, dass der Graph einer Funktion durchgängig gezeichnet werden kann. Der Graph hat also keine Polstelle oder macht "Sprünge". Das Epsilon Delta Kriterium besagt dass für alle Epsilon größer 0 ein Deltawert größer 0 existiert für alle x-Werte aus der Definitionsmenge. Dafür muss gezeigt werden dass der Betrag aus der Differenz von x und ein beliebiges x0 kleiner als Delta ist. Daraus folgt dann auch dass der Betrag der Funktionswerte aus x und x0 kleiner Epsilon ist.
AI generated image with ComfyUI and SDXL
Der Beweis erfolgt, indem man zunächst den Betrag der Funktion nimmt und diesen Umformt. Also anstelle von f(x) schreiben wir die Funktion und anstelle von f(x0) die Funktion nur mit dem Wert x0. Dann wird solange umgeformt bis man |x-x0| hat. Dieser Betrag muss kleiner als Delta sein. Dann setzen wir diesen Term gleich Epsilon und lösen nach Delta auf. Das Delta wird dann in der Ungleichung ersetzt und das Epsilon bleibt übrig was größer als der Betrag der Funktionswerte sein muss. Damit ist der Beweis vollbracht.
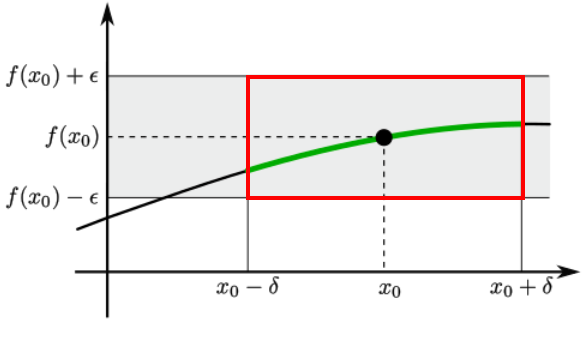
Mann kann sich das Epsilon Delta Kriterium wie ein Rechteck um den Graphen vorstellen. Um den Punkt x0 gibt es auf der x-Achse ein Delta größer 0 und um den Funktionswert f(x0) auf der y-Achse gibt es ein Epsilon größer 0, nur sind Epsilon und Delta sehr sehr klein. In dieser Grafik sind das Delta und Epsilon jetzt mal sehr groß. Wäre zum Beispiel das Delta sehr klein aber Epsilon deutlich größer, dann ist die Funktion am Punkt x0 nicht stetig, da der Funktionswert zu x0 ein Sprung auf der y-Achse macht. Der Graph ist also nicht durchgehend.
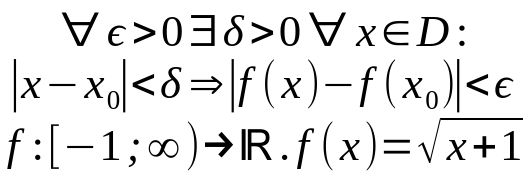
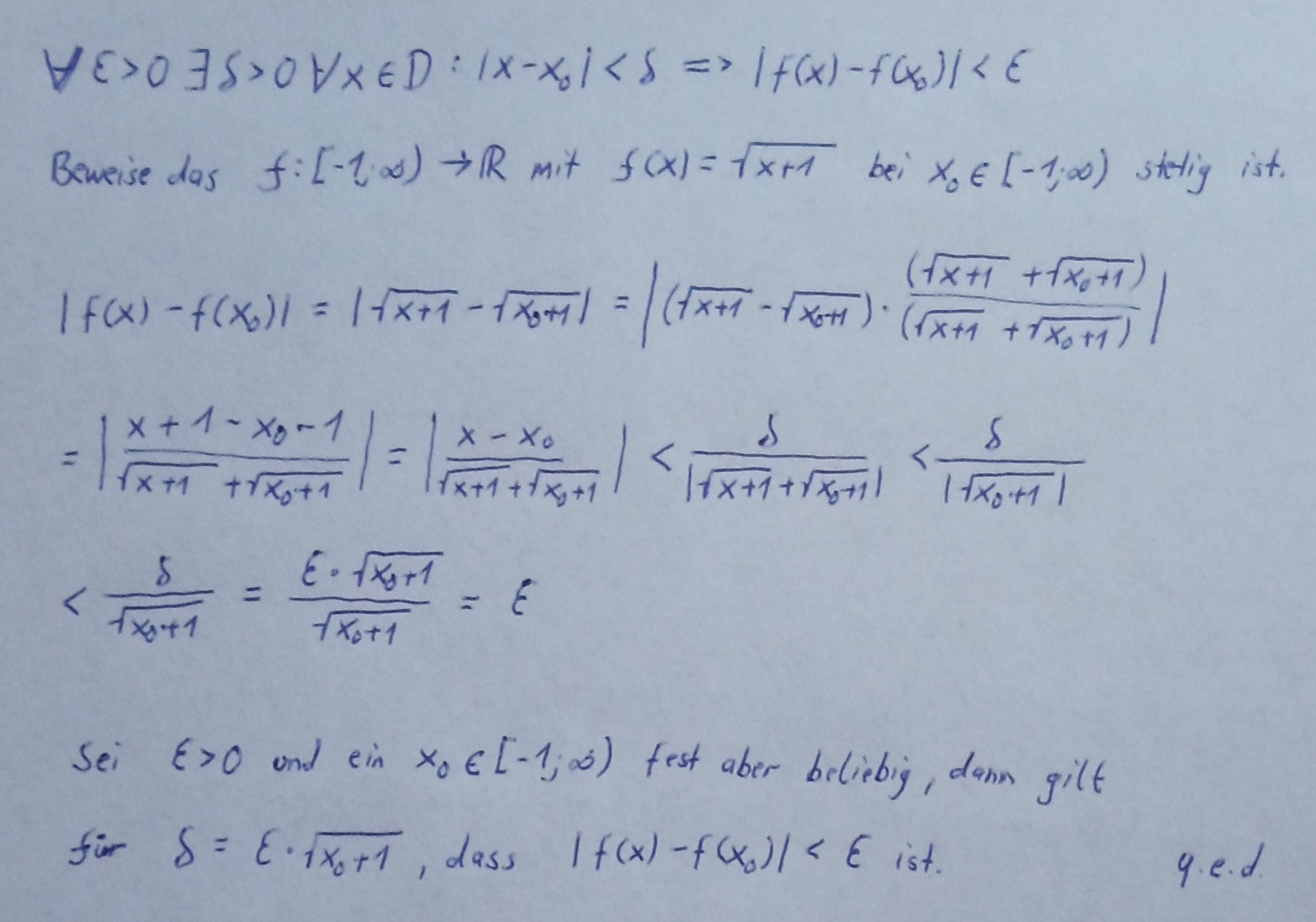
These photos were taken with my smartphone