Ein Sonderfall der Grenzwertrechnung ist das Anwenden der Regel von de L'Hospital. Erhält man als Grenzwert einen unbestimmten Ausdruck wie z.B. "unendlich/unendlich", "0/0", "0 mal unendlich"... dann kann man die Regel von de L'Hospital anwenden. Diese Regel besagt, dass man den Term im Zähler und Nenner ableitet und dann erneut den Grenzwert berechnet. Erhält man wieder einen unbestimmten Ausdruck, dann wird erneut abgeleitet.
Im ersten Beispiel haben wir im Zähler eine 0, denn e^1-e ist 0. Der ln(1) ist auch 0, also haben wir den Fall "0/0". Wir leiten e^x-e und ln(x) ab und versuchen erneut den Grenzwert zu bestimmen was geklappt hat. Der Grenzwert für x gegen 1 lautet e.
Das zweite Beispiel sieht einfach aus. Ich musste auch erstmal überlegen was ich mache, aber der Trick ist den gesamten Term als e-Funktion mit ln als Potenz umzuformulieren. Dadurch können wir die Potenzgesetzte anwenden, um die Potenz weiter zu vereinfachen. Dann versuchen wir den Grenzwert zu berechnen und sehen dass wir den Ausdruck "minus unendlich / minus unendlich" haben. Also ein Fall für L'Hospital. Nach dem Ableiten konnte die Potenz zu x vereinfacht werden. Nun war die Grenzwertermittlung einfach und wir erhalten 1.
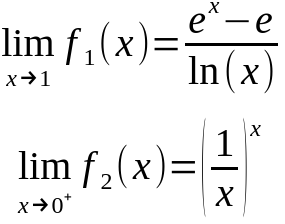
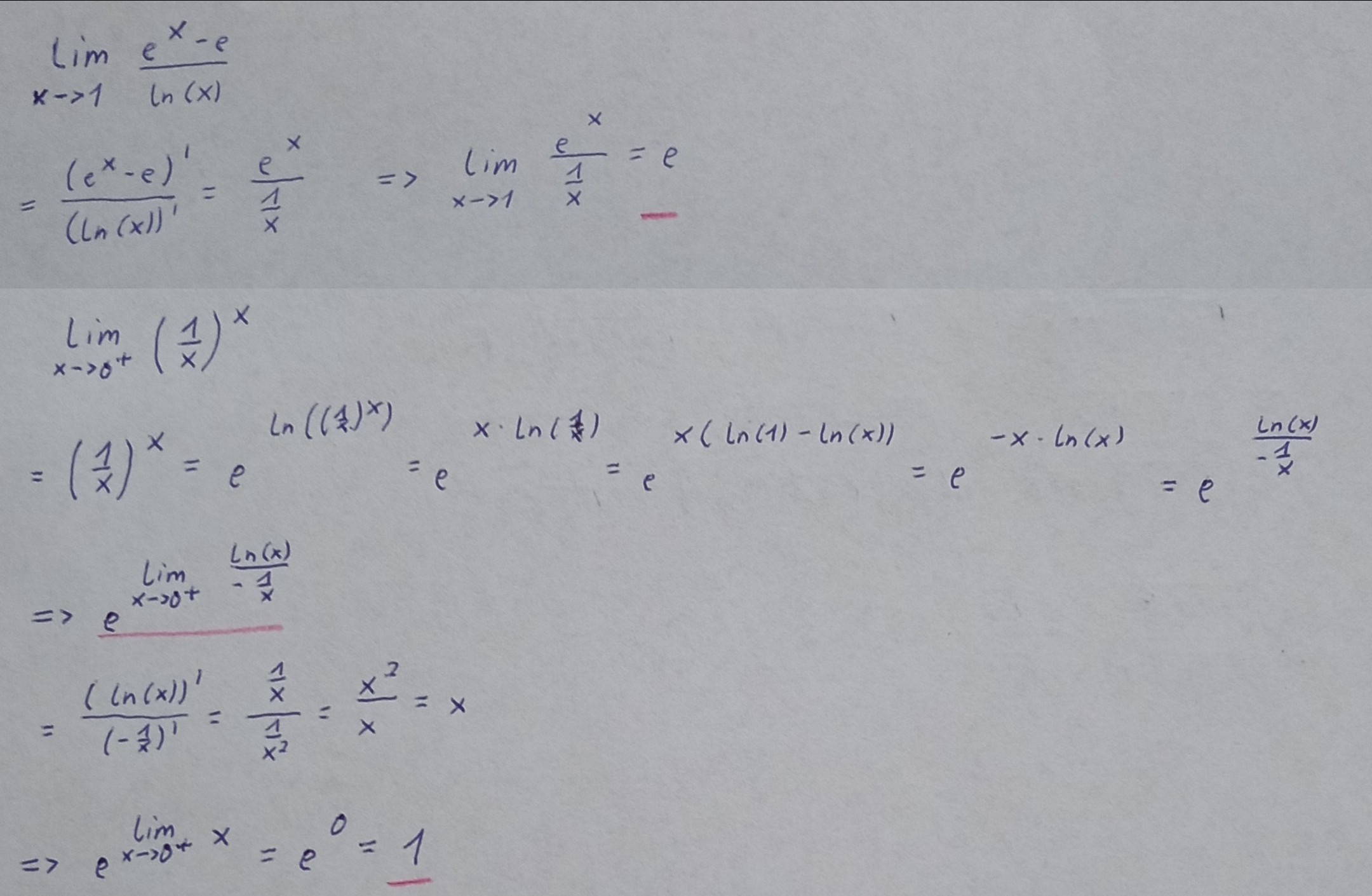
These photos were taken with my smartphone