Bei Ungleichungen mit einer Wurzel muss man zunächst den Definitionsbereich bestimmen. In diesem Beispiel ist der Radikant eine kubische Funktion. Von daher kann man nicht einfach davon ausgehen, dass nur alle x>=0 definiert sind. Das kann man machen wenn der Radikant nur aus x besteht.
Um den Definitionsbereich zu bestimmen berechnen wir die Nullstellen der kubischen Funktion. Die erste Nullstelle erhalten wir durch eine Polynomdivision. Anschließend wird die verbliebene quadratische Ungleichung gelöst. Durch die Nullstellen erhalten wir zwei Intervalle die miteinander Vereinigt werden. Jep, sieht nicht so schön aus aber wir haben unseren Definitionsbereich bestimmt.
Nun folgt die eigentliche Lösung der Wurzelungleichung mit der Bedingung, dass x>=2 ist. Für die Ermittlung der Nullstellen wird zuerst der Nullproduktsatz und dann die quadratische Ungleichung gelöst. Als vorläufige Lösungen erhalten wir -4,0 und 2. Jetzt müssen wir aber einmal den Definitionsbereich und die Bedingung berücksichtigen. Alle Lösungen befinden sich im Definitionsbereich. Das ist gut. Allerdings sagt die Bedingung, dass x>=2 sein muss. Von daher sind nur Zahlen zwischen 2 und unendlich gültige Lösungen für diese Wurzelungleichung.
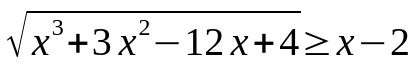
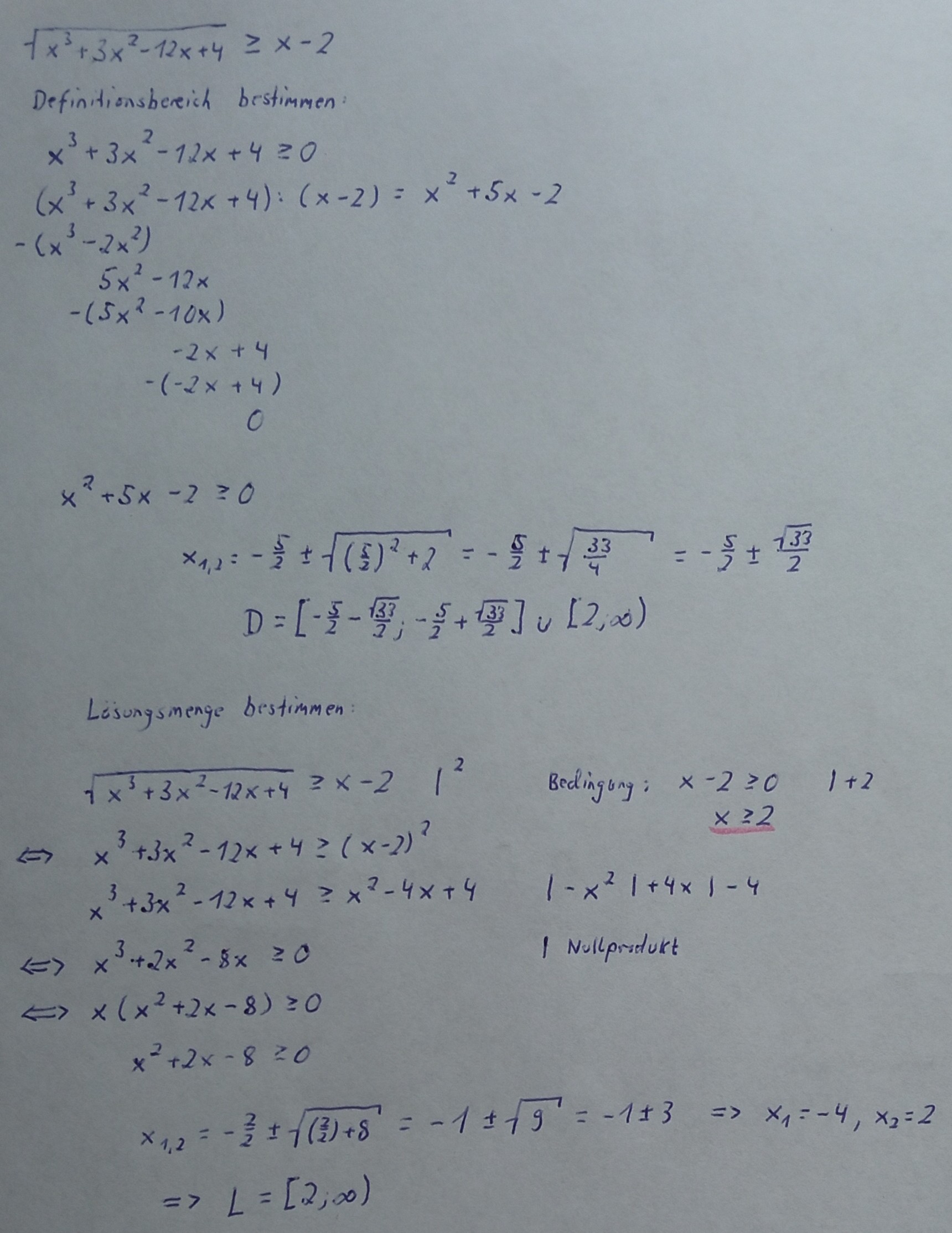
These photos were taken with my smartphone