Eine mathematische Reihe ist eine Summe mit unendlich vielen Summanden. Sie wird als ein großes Sigma mit einer Folge dargestellt. Unter dem Sigma steht der Startwert einer Variable. Über dem Sigma steht der Wert bis wohin summiert werden soll. Bei unendlichen Summen ist dieser Wert unendlich.
Solche Reihen können konvergieren oder divergieren. Eine konvergenz liegt vor, wenn die Summe sich einem Wert annähert. Wenn dies nicht der Fall ist, dann divergiert eine Reihe. Um zu untersuchen, ob eine Reihe konvergiert oder divergiert gibt es verschiedene Ansätze. Hier möchte ich ein Beispiel für das Majoranten- und Minorantenkriterium zeigen.
Übrigens kommen die Begriffe Minora und Majora ja auch noch woanders vor... ;) Ja ich weiss, der war nicht gut.
Weiter gehts. Die Idee hinter dem Majorantenkriterium ist, dass man eine gegebene Reihe abschätzt. Man versucht dass sich die gegebene Reihe an eine bereits bekannte Reihe, die auch konvergiert, sich annähert. Das abschätzen passiert in Zwischenschritten.
Mit dem Minorantenkriterium kann man zeigen, dass eine Reihe divergiert. Welches der beiden Kriterien für eine Reihe anwendet wird muss man ausprobieren. Funktioniert das Abschätzen mit dem Majorantenkriterium nicht, so nimmt man das Minorantenkriterium.
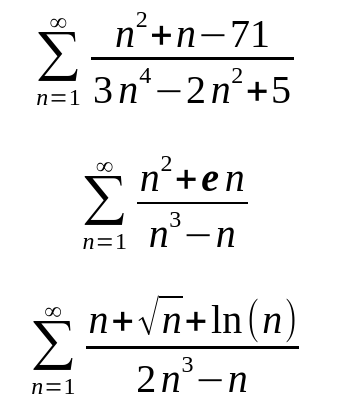
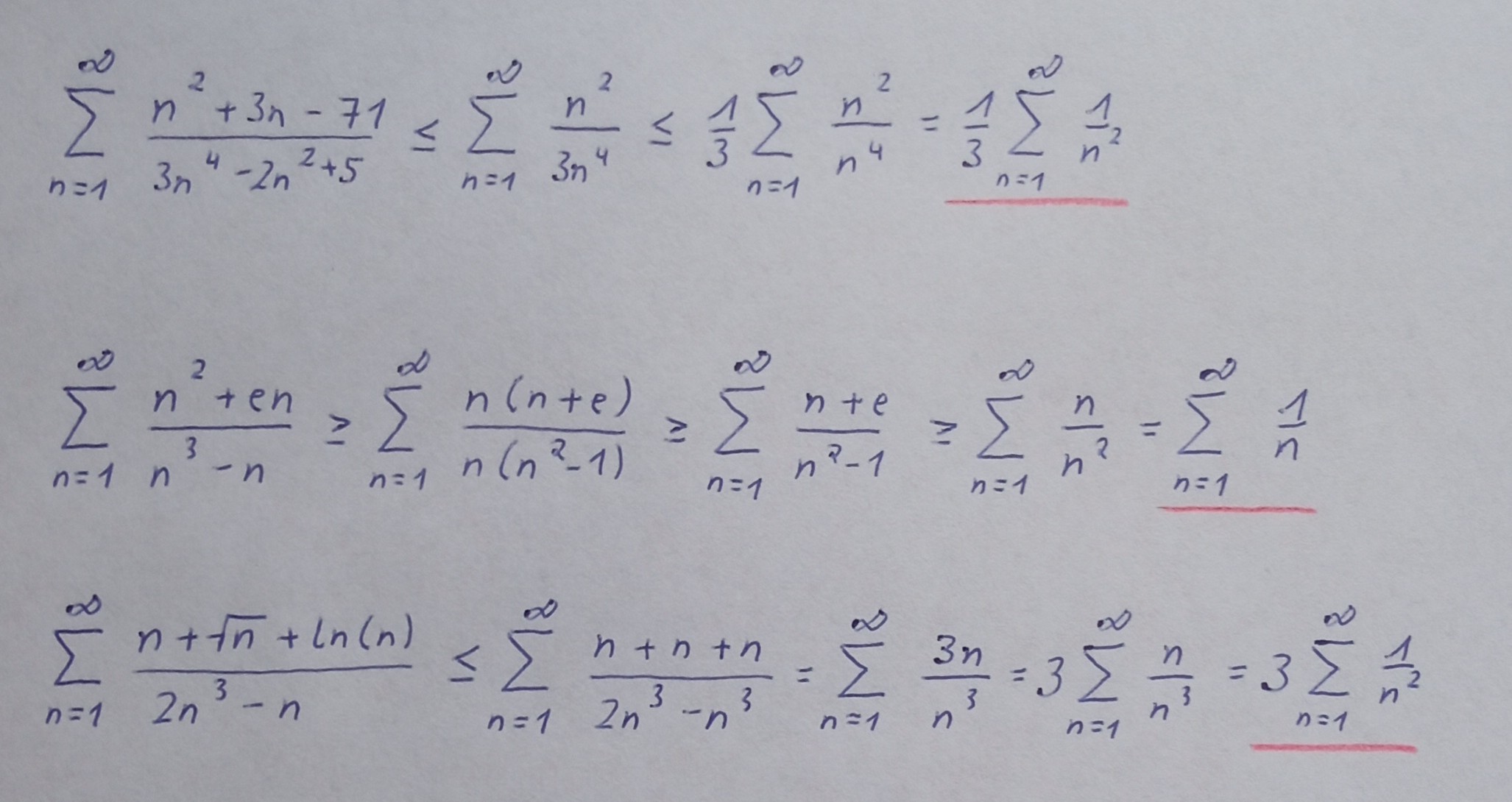
These photos were taken with my smartphone