Nach dem Beweis der Stetigkeit einer Funktion mit dem Epsilon Delta Kriterium, möchte ich hier rechnerisch zeigen wie man die Stetigkeit einer zusammengesetzten Funktion mit dem Limes überprüft.
Damit eine Funktion am Punkt x0 stetig ist, müssen der links- und rechtsseitige Limes gleich sein. Das wars schon. Bei einer Ungleichheit ist die Funktion am Punkt x0 unstetig.
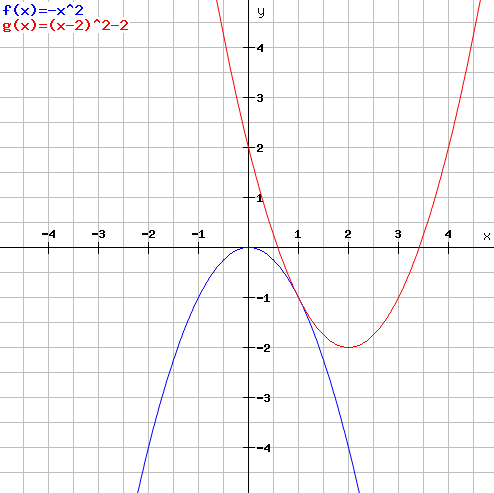
Im dritten Beispiel wird ein Sonderfall betrachtet, dass Parameter die Stetigkeit einer Funktion beeinflussen. Um die Parameter zu bestimmen, müssen wir wie in den ersten beiden Beispielen die Limes bestimmen. Übrig bleiben noch die Parameter nach denen man die Gleichung auflöst. Das Ergebnis sind dann die Werte bei denen die parametrisierte Funktion stetig ist. Bei allen anderen Werten ist die Funktion unstetig.
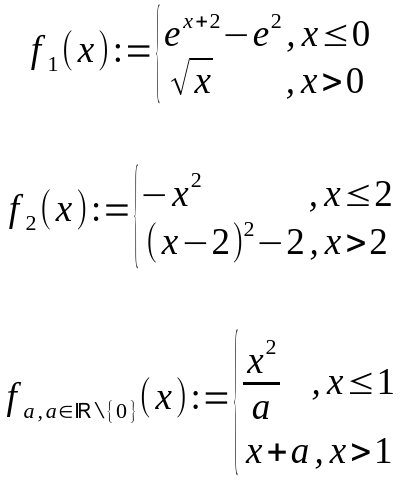
Funktionsgraph zu f1
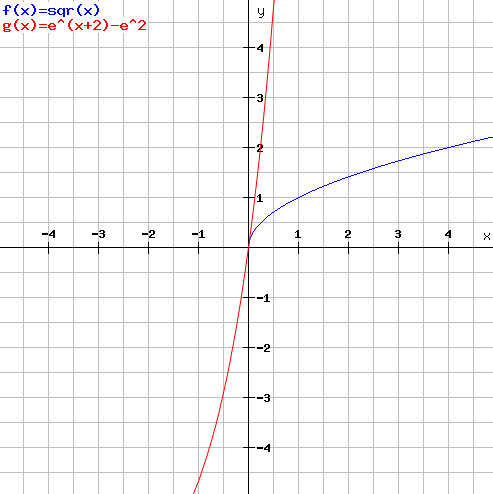
Funktionsgraph zu f2
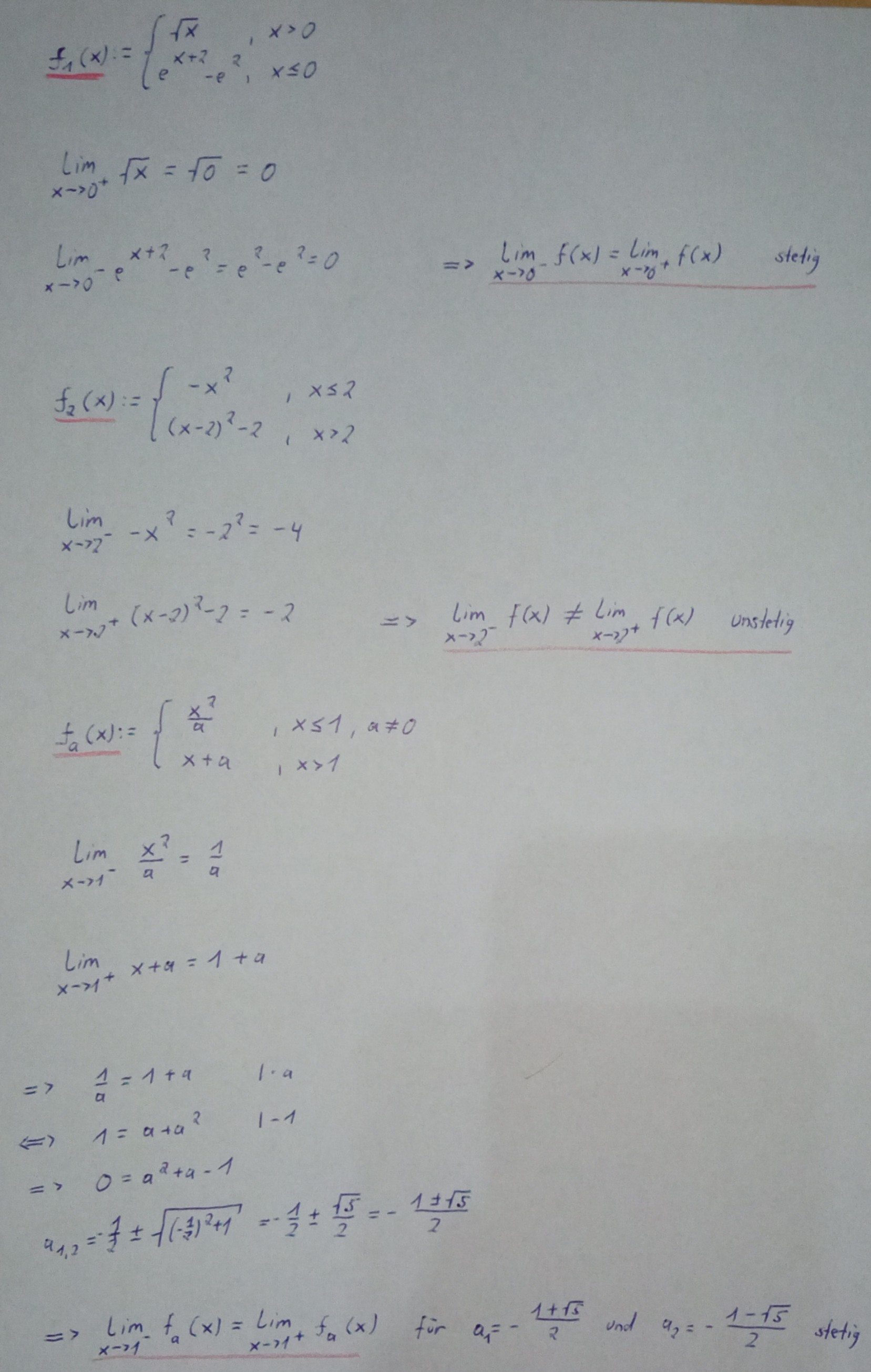
These photos were taken with my smartphone