Mit dem Taylorpolynom kann man jede beliebige komplizierte Funktion näherungsweise durch eine Polynomfunktion vom Grad n bestimmen. Je höher die Ordnung des Taylorpolynom, desto genauer nähert sich das Polynom an die originale Funktion an dem Entwicklungspunkt x0 an.
Taylorpolynome kann man zum Beispiel verwenden, wenn die Berechnung einer Funktion zu kompliziert ist und man sich mit einem ungefähren Ergebnis zufrieden gibt. Gerade in der Programmierung kann dies hilfreich sein, z.B. eine Polynomfunktion zu berechnen, anstelle einer Verkettung eines Arcustangens mit einer Wurzel mit Logarithmus als Radikant oder ähnliches.
Die verkettete Funktion x^2*ln(x) soll mit einem Taylorpolynom 4. Ordnung und mit Entwicklungspunkt 1 näherungsweise bestimmt werden. Dafür differenziert man die Funktion f insgesamt 4 mal. Anschließend wird der Entwicklungspunkt als Funktionswert aller Ableitungen einschließlich der Ausgangsfunktion berechnet. Nun kann schon das Taylorpolynom ermittelt werden.
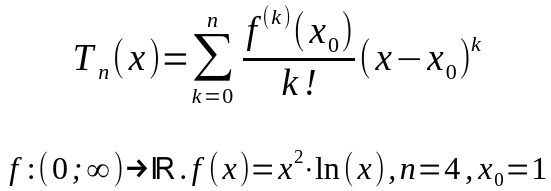
Ich habe mir die Mühe gemacht, um alle Klammern auszumultiplizieren. In der Grafik sieht man den Vergleich der Originalfunktion f und dem Taylorpolynom T. Beachte den Entwicklungspunkt. Beide Funktionen überschneiden sich ungefähr im Interval [0,25;2]. Die Wertetabelle zeigt die Genauigkeit in diesem Interval.
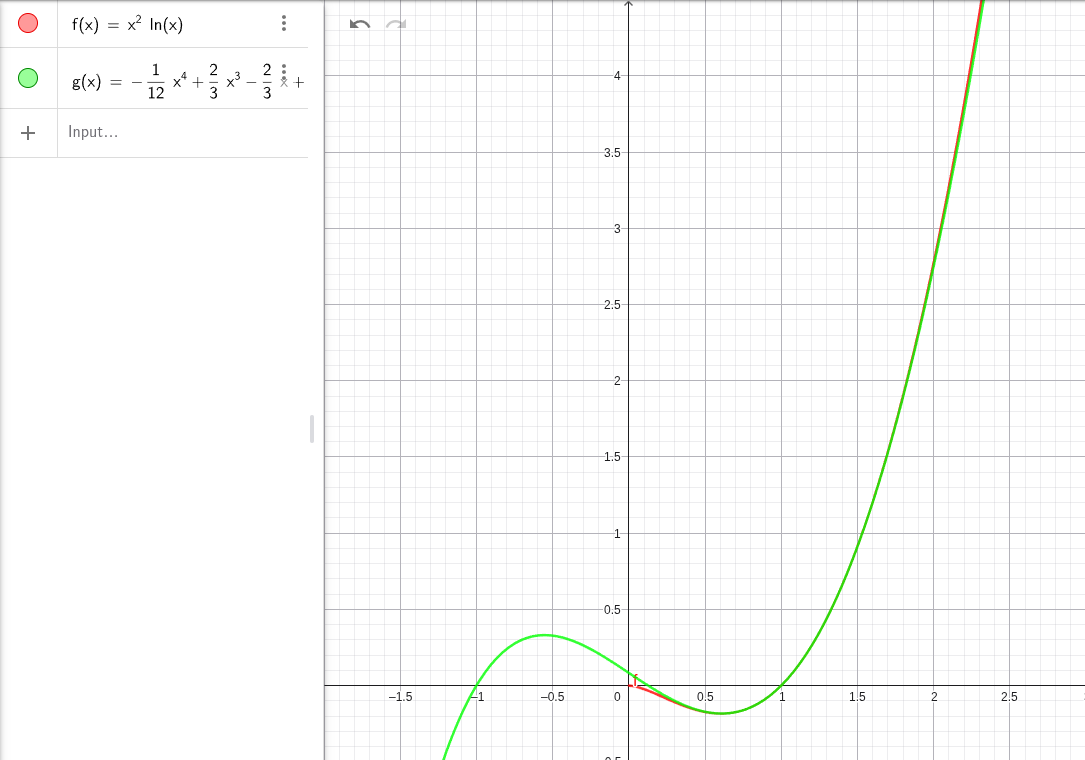f(x) Original, g(x) Taylorpolynom
These photos were taken with my smartphone