Liebe Leser, schon seit Jahrtausenden streiten sich die Gelehrten, ob es so etwas wie Unendlichkeit überhaupt gibt. In der Theorie kann man sich leicht unendliche Dinge ausmalen, schon allein die Menge der natürlichen Zahlen ist unendlich, da man auch zu der allergrößten denkbaren immer noch 1 dazuzählen kann. Auch irrationale Zahlen wie π oder √2 haben unendlich viele Stellen hinter dem Kommazeichen. Irrational nicht, weil diese Zahlen wider die Vernunft sind, sondern weil sie sich nicht als Bruch (=Verhältnis, ratio) zweier ganzer Zahlen darstellen lassen. Warum die liegende 8, ∞ für unendlich steht (1655 erstmals benutzt vom englischen Mathematiker John Wallis), ist übrigens nicht ganz klar. Meine Theorie: Sie symbolisiert eine Möbiusschleife, die bekanntlich auch endlos ist. Seltsam nur, dass das Möbiusband erst im 19.Jhd. erfunden wurde!
Vor 2300 Jahren hatte aber schon Aristoteles unterschieden zwischen einer potentiellen und einer tatsächlichen ("aktualen") Unendlichkeit. Letztere hielt er für unmöglich. Spätere Denker haben diese Sichtweise übernommen und auch als Gottesbeweis genutzt, denn die Erklärbarkeit der Realität ist auf diese Weise undurchführbar, weil die Ursachenkette nie aufhört, also unendlich sein müsste (z.B. was war vor dem Urknall? Ein voriges Universum, aber wie ist das entstanden? Auch mit einem Urknall, usw.). Stattdessen wird Gott als Erstursache angenommen, die selbst nicht Teil einer Ursachenreihe ist. Aus meiner Sicht nicht seht überzeugend, denn warum sollte Gott nicht auch einen Schöpfer haben bzw. wie kann etwas existieren, ohne geschaffen worden zu sein? Mathematik, Philosophie und Religion verschwimmen hier zu etwas (für uns Menschen) ziemlich Unentwirrbarem! Andere behaupteten auch, Gott ist die Unendlichkeit! Aber für die Beantwortung der Frage, ob sie existiert, hilft uns diese Aussage auch nicht weiter.
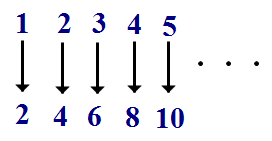
Erst der Erfinder der Mengenlehre, der deutsche Mathematiker Georg Cantor (1845-1918), führte das Rechnen mit Unendlichkeit(en) in die Mathematik ein. Es gibt (mathematische) Unendlichkeiten und andere, noch größere Unendlichkeiten! Er fand also heraus, dass nicht jede unendliche Menge gleich groß ist. Zum Beispiel ist die Menge aller reeller Zahlen größer als die Menge der natürlichen Zahlen, obwohl beide unendlich groß sind! Klingt soweit logisch, denn alleine zwischen 0 und 1 gibt es unzählbar viele Dezimalzahlen, sodass man nicht einmal sagen kann, was die kleinste ist: 0,000000001 oder 0,0000000001 oder 0,000000000000000000001? Aber die Menge der geraden Zahlen {2, 4, 6,...}, die gefühlt eigentlich nur halb so groß sein sollte wie die der natürlichen Zahlen N {1, 2, 3,...}, ist es nicht. Beide Mengen sind gleich groß, oder um es mathematisch auszudrücken, gleichmächtig bzw. sie haben die gleiche "Kardinalität"! Warum? Weil zwischen beiden Mengen eine "Bijektion" besteht, d.h. es gibt zu jedem Element von N genau ein Element in der Menge der geraden Zahlen, über die Funktion f(n)=2n. D.h. jede natürliche Zahl lässt sich verdoppeln und das Ergebnis ist immer eine gerade Zahl, daher müssen beide Mengen gleich groß sein.
 https://sburchette.wordpress.com/2015/05/30/infinity-part-1/
https://sburchette.wordpress.com/2015/05/30/infinity-part-1/
Sogar die Menge aller positiver rationaler Zahlen (Q+), also N plus aller Zahlen, die sich als Bruch mit ganzen Zahlen darstellen lassen (1/2, 1/3, 5/99, usw.) ist nicht größer als die Menge der natürlichen Zahlen, so widersinnig das auch erscheinen mag! Auch zwischen Q+ und N gibt es eine Bijektion, wie Cantor nachwies, aber der Beweis würde jetzt zu weit führen.
Andere, scheinbar unlogische Konsequenzen der Mengenlehre unendlicher Mengen sind das Hyperwebster-Paradox (hier erklärt) und das Banach-Tarski Paradox, wonach man eine Kugel derart in kleinste Teile zerlegen kann, dass sich diese Teile wieder zu zwei Kugeln zusammenfügen lassen, die beide gleich groß sind wie die ursprüngliche! Aus diesen Gründen haben einige Mathematiker an diesem Konzept gezweifelt und diese Form der Unendlichkeit abgelehnt - Finitismus genannt (vom engl. finite = endlich).
Die Finitisten behaupten, dass ein mathematisches Objekt nur existiert, wenn es mit einer endlichen Anzahl von Schritten aus den natürlichen Zahlen konstruiert werden kann. Irrationale Zahlen dagegen, selbst wenn sie mit eindeutigen Formeln wie √2 berechnet werden können, bestehen aus unendlichen Zahlenfolgen und können daher nicht Teil der endlichen Mathematik sein. Auch der Satz vom ausgeschlossenen Dritten (der besagt, dass für jede Aussage nur die Aussage selbst oder ihr Gegenteil gelten kann, nichts Drittes) gilt für Finitisten nicht, für sie kann eine Aussage nicht nur wahr oder falsch sein, sondern unbestimmt zu einem bestimmten Zeitpunkt, wenn der korrekte Wert einer Zahl (noch) nicht berechnet wurde. Z.B. die Zahl 0,999... (mit unendlich vielen Nachkommastellen) ist laut klassischer Mathematik 1. Für Finitisten ist das nicht so, denn unendlich viele Nachkommastellen gibt es nicht für sie!
Ohne die Unendlichkeit wird die Mathematik aber um Einiges komplizierter, denn viele Theoreme beruhen z.B. auf dem Satz vom ausgeschlossenen Dritten. Der Finitismus hat daher nur wenige Anhänger. Aber könnte nicht gerade der Finitismus Raum und Zeit sogar besser erklären, wenn man annimmt, dass der Weltraum eben nur eine endliche Information und Teilchenmenge beinhalten kann und dass Unendlichkeit eher eine Abstraktion als Realität ist?
Die Physik des ganz Großen und ganz Kleinen, die Kosmologie und die Quantenphysik scheinen derzeit in einer Sackgasse zu stecken. Immer wieder tauchen beunruhigende neue Erkenntnisse auf, die im Widerspruch zum Standardmodell der Kosmologie stehen (Beispiel, Beispiel) und es gibt keinerlei Konsens darüber, wie die Quantenphänomene überhaupt zu interpretieren sind (Quelle), daher wäre ein neuer Erklärungsansatz, der radikal mit der klassischen Mathematik bricht, eventuell einen Versuch wert...

Quellen: https://de.wikipedia.org/wiki/Potentielle_und_aktuale_Unendlichkeit https://www.scientificamerican.com/article/what-if-infinity-didnt-exist/ https://www.scientificamerican.com/article/infinity-is-not-always-equal-to-infinity/ https://journals.aps.org/pra/abstract/10.1103/PhysRevA.100.062107 https://uneedtonoparadox.blogspot.com/2016/05/the-hyperwebster-dictionary.html https://youtu.be/s86-Z-CbaHA?si=9bGMk8idfjFfPxE1