~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

06-09-2025 - Operations Research - The Polyhedron [EN]-[IT] With this post, I would like to provide a brief introduction to the topic in question. (lesson/article code: MS_08)

Image created with artificial intelligence, the software used is Microsoft Copilot
Introduction The polyhedron is a fundamental topic in linear programming. The polyhedron represents the set of points that satisfy a finite number of linear equations or inequalities (linear means that we have no variables with exponents, i.e., the curves drawn by the constraints and variables are all straight lines). NOTE: In the plane, the extreme points of a polyhedron are its vertices.
Importance of the Polyhedron In linear programming, the polyhedron is important for the following reasons: -The graph of the polyhedron shows the feasible regions; that is, the set of x's that satisfy the constraints will form a polyhedron. -The endpoints or vertices of the polyhedron are important points because they are the basic feasible solutions.
Example Let's try an example with the following linear programming problem.
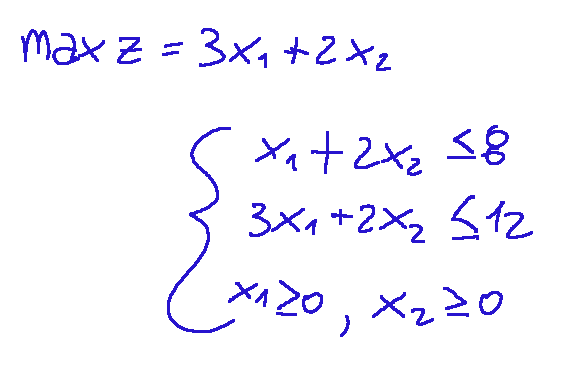
The polyhedron of the exercise The polyhedron of the exercise is shown below.
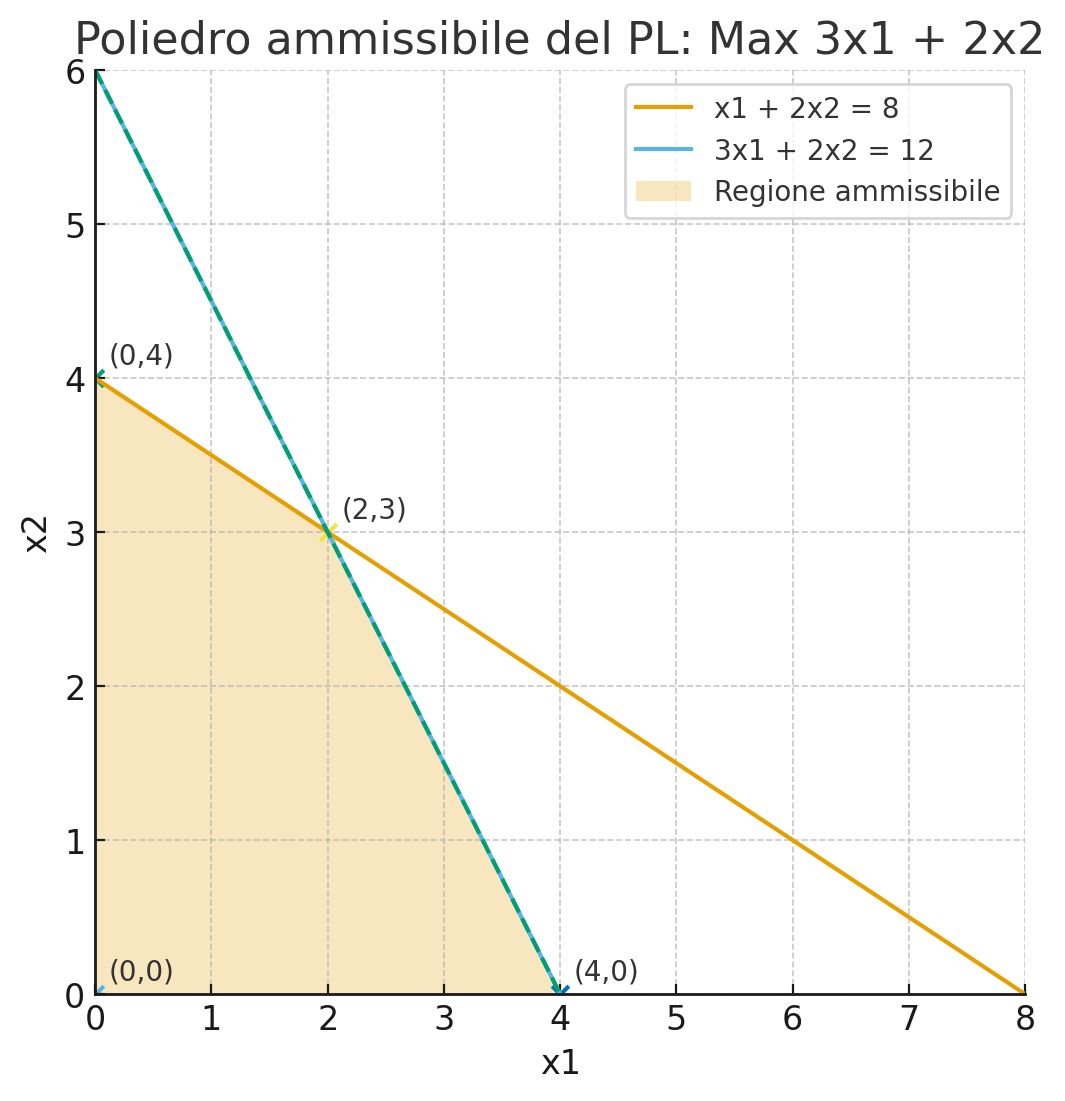
Image created with artificial intelligence, the software used is ChatGPT
To find the To draw a polyhedron, we first draw the line that identifies x1 + 2x2 <= 8, which is the first term of our system, or rather, the first constraint. To draw a line, we need two points, and when we want to draw a line in linear programming, we set the variables to ZERO. So, in this case, we get the following, considering the equation of the first constraint. first constraint equation
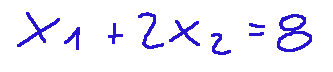
From this simple equation, we can understand the values of x1 and x2.
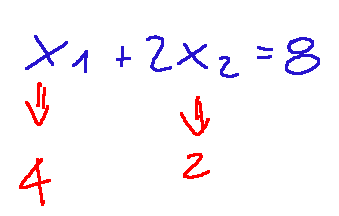
So if we set the variables to zero, we will find the intercepts on the axes, first on x1 and then on x2
First I set x2=0
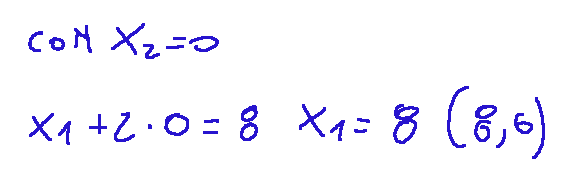
Then I set x1=0
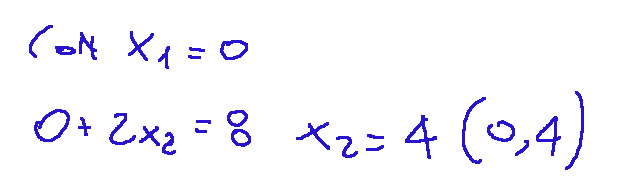
At this point I have a line with the points (8,0) and (0,4) In the graph I will draw The following line highlighted in yellow
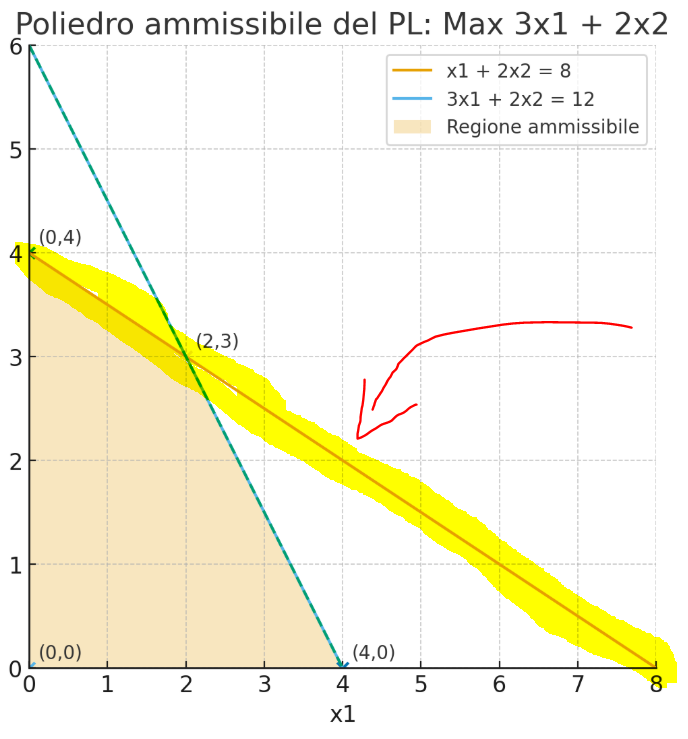
I then use the same method to draw the other line, and I'll have a shared space bounded by the intersection of the lines. The orange-colored area of the graph is the feasible region. The feasible region is the area of the graph that satisfies all the constraints simultaneously.
The Feasible Region The feasible region is the set of points that satisfy all the constraints; in the graph, it is the shaded, closed, and convex area bounded by the two lines and the axes in the first quadrant. The feasible region is therefore our polyhedron.
Conclusions A polyhedron is the intersection of linear half-spaces and describes the feasible region of a linear programming problem. The vertices of the polyhedron correspond to the basic feasible solutions, and one of these vertices is the linear optimum, that is, the optimal solution.
Question Did you know that it was the American mathematician George Dantzig (1914-2005) who combined the concept of linear programming with that of the polyhedron? Did you know that George Dantzig is considered the father of linear programming? Did you also know that linear programming is closely linked to the birth of the first electronic computers? Did you know that the first electronic computers (around 1950) were used precisely to perform linear programming calculations?

ITALIAN

06-09-2025 - Ricerca operativa - il poliedro [EN]-[IT] Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto (codice lezione/articolo: MS_08)

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione Il poliedro in programmazione lineare è un argomento fondamentale. Il poliedro rappresenta l'insieme di punti che soddisfano un numero finito di equazioni o disequazioni lineari (lineari significa che non abbiamo variabili con esponenti, cioè che le curve disegnate dai vincoli e dalle variabili sono tutte rette) NOTA: Nel piano i punti estremi di un poliedro Sono i vertici del poliedro.
Importanza del poliedro Nella programmazione lineare il poliedro è importante per i seguenti motivi: -Il grafico con il poliedro mostra le regioni ammissibili, cioè l'insieme delle x che rispettano i vincoli formerà un poliedro. -Gli estremi o i vertici del poliedro sono punti importanti perché sono le soluzioni di base ammissibili.
Esempio Proviamo a fare un esempio con il seguente problema di programmazione lineare.
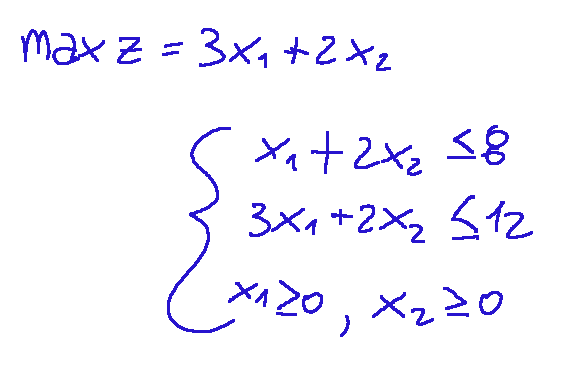
Il poliedro dell'esercizio Qui di seguito è mostrato il poliedro dell'esercizio

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Per trovare il poliedro si traccia prima la retta che identifica da x1+2x2<=8, cioè il primo termine del nostro sistema, o meglio il primo vincolo. Per tracciare una retta abbiamo bisogno di due punti e quando vogliamo tracciare una retta in programmazione lineare poniamo le variabili a ZERO. Quindi in questo caso avremo quanto segue pensando all'equazione del primo vincolo. equazione del primo vincolo
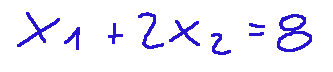
Da questa semplice equazione possiamo comprendere i valori di x1 e x2
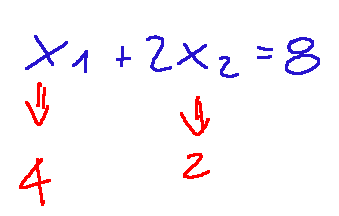
Quindi se poniamo le variabili a zero troveremo le intercette sugli assi, prima su x1 e poi su x2
prima metto x2=0
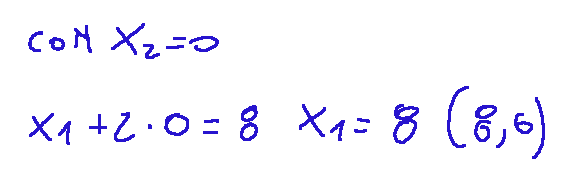
poi metto x1=0
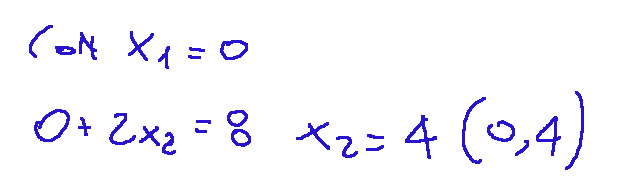
a questo punto ho una retta con i punti (8,0) e (0,4) Nel grafico traccerò la seguente retta evidenziata in giallo

Uso poi lo stesso metodo per tracciare l'altra retta e avrò uno spazio in comune delimitato dall'incrocio delle rette. L'area del grafico colorata di arancione è la regione ammissibile. La regione ammissibile è l’area del grafico che soddisfa tutti i vincoli contemporaneamente.
La regione ammissibile La regione ammissibile è l’insieme dei punti che rispettano tutti i vincoli; nel grafico è l’area ombreggiata, chiusa e convessa, delimitata dalle due rette e dagli assi nel primo quadrante. La regione ammissibile è quindi il nostro poliedro.
Conclusioni Un poliedro è l’intersezione di semispazi lineari ed esso descrive la regione ammissibile di un problema di programmazione lineare. I vertici del poliedro corrispondono alle soluzioni di base ammissibili e uno di questi vertici è l'ottimo lineare, cioè la soluzione ottimale.
Domanda Lo sapevate che fu il matematico statunitense George Dantzig (1914-2005) ad unire il concetto della programmazione lineare con quella del poliedro? Sapevate che George Dantzig è ritenuto il padre della programmazione lineare? Sapevate anche che la programmazione lineare è strettamente legata alla nascita dei primi computer elettronici? Sapevate che primi computer elettronici (1950 circa) furono usati proprio per eseguire calcoli di programmazione lineare?
THE END