
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

12-08-2025 - Mechanics - Real, Physical, and Mathematical Systems [EN]-[IT] With this post, I would like to provide a brief introduction to the topic mentioned above. (code notes: X_96)
Mechanical Systems

Image created with artificial intelligence, the software used is Microsoft Copilot
Introduction First, let's define what a mechanical system is. It is a set of rigid or deformable bodies connected to each other and subject to forces, constraints, and motions.
What are forces, constraints, and motions
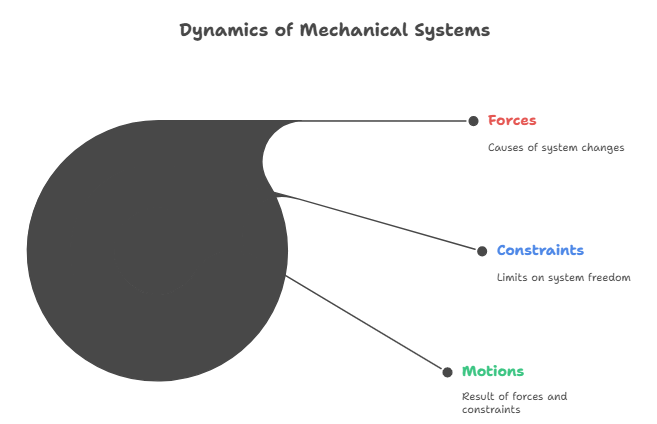
Image created with artificial intelligence, the software used is Napkin.ai
Forces are the causes that tend to vary the state of the system and can be external forces, driving forces, torques, spring forces, and damping forces. Constraints are what limit the degrees of freedom of the mechanical system, such as a plane hinge, support constraints that prevent vertical translations but allow rotations, or fixed constraints. Motions are what happens after forces are applied to the mechanical system, which will move according to the designed constraints.
We can summarize this by saying: Forces are the cause of motion or deformation, constraints impose limits on motion, while motions are the result of the interaction between forces and constraints.
Note: A constraint is external if it is due to the presence of other bodies. A constraint is said to be nonholonomic if it is a function of the velocities of the bodies.
Real System and Physical Model
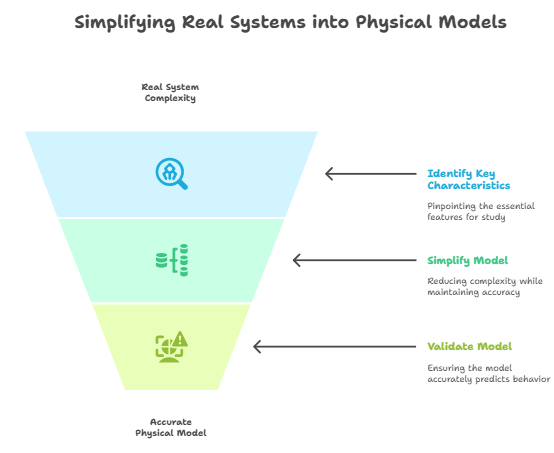
Real System The real system is the object or group of objects as they exist in the physical world, that is, as it is in reality and subject to complex phenomena. Physical Model The physical model is a simplified representation of the real system and is designed to study its behavior. The Transition from a Real System to a Physical System Let's clarify the concept of a physical system again so as not to lose track of the discussion; I'll try to use different terms. A physical model of a real system means an imaginary physical system that is equivalent to the real system, given certain characteristics relevant to the study, within a predefined operating range. However, we must consider one important thing: the physical model must be simple, but it must accurately and satisfactorily predict the behavior of the real system. At this point, we can deduce that to make the transition from the real system to the physical one, we must make approximations. Below is a list of the approximations that can be made. -1- Neglect small effects, that is, eliminate interactions between components or between the system and the outside world that cause negligible effects on the system's behavior; -2- Assume that the system does not modify the external environment and therefore does not simultaneously vary the effect of the environment on the system; -3- Substitute concentrated characteristics for distributed characteristics (ordinary differential equations instead of partial differential equations); -4- Allow linear dependence between variables (e.g., springs assumed to be linear even though they are not); -5- Assume time-invariant parameters; -5- Ignore uncertainties and disturbances.
From the physical model to the mathematical model
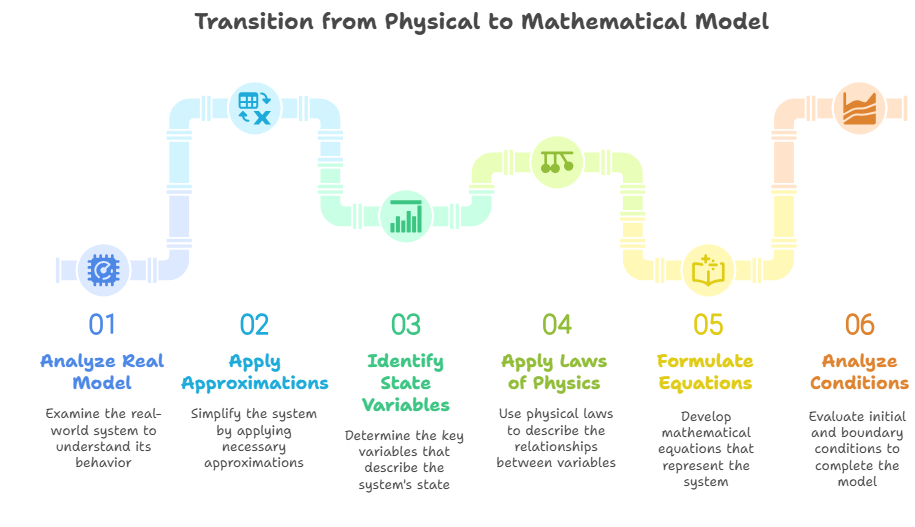
Image created with artificial intelligence, the software used is Napkin.ai
Once we have the physical model, that is, after analyzing the real model by applying approximations, we can prepare the mathematical model. From physical system to mathematical model To perform this step, you must: Identify the state or motion variables Apply the laws of physics Start thinking about the differential or algebraic equations that identify the system Analyze the initial and boundary conditions carefully.
Ultimately, the mathematical model is the numerical version of the physical model.
Conclusions In applied mechanics, a real system is considered to be a concrete system that exists in reality; a physical system is a simplification of the real system (where only the relevant aspects are considered); and finally, a mathematical system is the representation of the physical system through equations, variables, and mathematical models.
Question Did you know that the concept of a mathematical model based on differential equations was introduced by Isaac Newton? Did you know that his laws of motion allow us to rigorously describe the dynamic behavior of bodies?

ITALIAN

12-08-2025 - Meccanica - Sistema reale, fisico e matematico [EN]-[IT] Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto (code notes: X_96)
Sistemi meccanici

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione Innanzitutto definiamo cosa è un sistema meccanico. Esso è un insieme di corpi rigidi o deformabili collegati tra loro e soggetti a forze, vincoli e moti.
Cosa sono le forze, vincoli e moti

immagine creata con l’intelligenza artificiale, il software usato è Napkin.ai
Le forze sono le cause che tendono a variare lo stato del sistema e possono essere forze esterne, forze motrici, momenti torcenti, forze elastiche e forze di smorzamento. I vincoli sono ciò che limita i gradi di libertà del sistema meccanico come una cerniera piana, vincoli di appoggio che impedisce traslazioni verticali ma consente rotazioni oppure vincoli fissi. I moti sono ciò che succede dopo che vengono applicate le forze al sistema meccanico che si muoverà a seconda dei vincoli progettati.
Possiamo riassumere dicendo questo. Le forze sono la causa del moto o della deformazione, i vincoli impongono limiti al moto, mentre i moti sono il risultato dell’interazione tra forze e vincoli.
Note: Un vincolo è esterno se è dovuto alla presenza di altri corpi. Un vincolo è detto anolonomo se è funzione delle velocità dei corpi.
Sistema reale e modello fisico

Sistema reale Il sistema reale è l’oggetto o il gruppo di oggetti così come esistono nel mondo fisico, cioè come è nella realtà e soggetto a fenomeni complessi. Modello fisico Il modello fisico è una rappresentazione semplificata del sistema reale ed è ideato per studiarne il comportamento. Il passaggio da sistema reale a quello fisico Chiariamo nuovamente il concetto di sistema fisico per non perdere il filo del discorso, provo ad usare delle parole diverse. Con modello fisico di un sistema reale si intende un sistema fisico immaginario che sia equivalente al sistema reale, per certe sue date caratteristiche riguardanti lo studio, in un campo di funzionamento prestabilito. Dobbiamo però considerare una cosa importante, cioè il modello fisico deve essere semplice, ma deve prevedere in maniera accurata e soddisfacente il comportamento del sistema reale. A questo punto possiamo dedurre che per effettuare il passaggio dal sistema reale a quello fisico dobbiamo fare delle approssimazioni. Qui di seguito un elenco delle approssimazioni che possono essere fatte. -1- Trascurare i piccoli effetti, ovvero eliminare le interazioni tra componenti o fra il sistema e l’esterno che provochino effetti trascurabili sul comportamento del sistema; -2- Ammettere che il sistema non modifichi l’ambiente esterno e non vari quindi allo stesso tempo l’azione dell’ambiente sul sistema; -3- Sostituire caratteristiche concentrate a caratteristiche distribuite (equazioni differenziali ordinarie invece che alle derivate parziali); -4- Ammettere dipendenza lineare tra le variabili (es: molle considerate lineari anche se in realtà non lo sono); -5- Assumere parametri tempo-invarianti; -5- Trascurare incertezze e disturbi.
Dal modello fisico al modello matematico

immagine creata con l’intelligenza artificiale, il software usato è Napkin.ai
Una volta giunti al modello fisico, cioè dopo aver analizzato il modello reale applicando delle approssimazioni, possiamo preparare il modello matematico. da sistema fisico e al modello matematico Per effettuare questo passaggio bisogna: Identificare le variabili di stato o di moto Applicare le leggi della fisica Iniziare a pensare alle equazioni differenziali o algebriche che identificano il sistema Analizzare bene le condizioni iniziali e di contorno.
In definitiva il modello matematico è la versione numerica del modello fisico.
Conclusioni In meccanica applicata viene considerato come sistema reale il sistema concreto che esiste nella realtà, il sistema fisico è una semplificazione del sistema reale (dove sono considerati solo gli aspetti rilevanti) ed infine il sistema matematico è la rappresentazione del sistema fisico tramite equazioni, variabili e modelli matematici.
Domanda Lo sapevate che il concetto di modello matematico basato su equazioni differenziali fu introdotto da Isaac Newton? Lo sapevate che le sue leggi del moto permettono di descrivere il comportamento dinamico dei corpi in modo rigoroso?
THE END
immagine creata con l’intelligenza artificiale, il software usato è Napkin.ai