
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

27-08-2025 - Mechanics - Fundamental Equations of Motion [EN]-[IT] With this post, I would like to provide a brief introduction to the topic in question. (lesson/article code: LE_90)

Image created with artificial intelligence, the software used is Microsoft Copilot
Introduction In applied mechanics, the fundamental equations of motion describe how the position, velocity, and acceleration of a body vary as a function of time. In this article, I will discuss some of them without going into detail, but I will nevertheless provide a general description, so as to have a sort of collection of the most important and well-known ones.
The starting point for the study of the fundamental equations of motion is Newton's law, or the second law of motion. It establishes the connection between shape and acceleration. Technically, the second law of motion states that the resultant of the forces applied to a body is equal to the product of the body's mass and its acceleration. The law we're talking about is shown below.
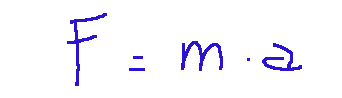
Translational and Rotational Motion Let's remember the following before starting the series of formulas. Translational Motion Motion is called translational when the orientation of the body remains constant. In translational motion, all points have the same velocity and acceleration. Rotational Motion Rotational motion occurs when a rigid body rotates around a fixed axis and all its points move along circular paths.
Uniformly Accelerated Rectilinear Motion The kinematic relations for uniformly accelerated rectilinear motion derive from the second law of dynamics. Below I show the three most important kinematic relationships:
Time Law
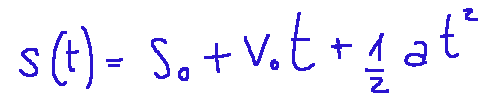
Velocity

Direct relationship between velocity and space
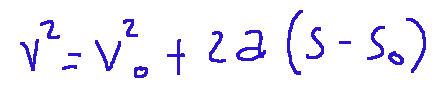
Galileo's Theorem Galileo's theorem tells us that the velocity of a point on a rigid body is the sum of the velocity of a chosen point plus a term related to rotation.
It includes two formulas. First formula
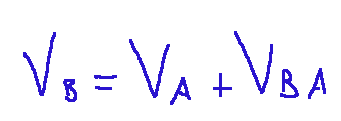
This formula tells us that the velocity of point B of a rigid body is obtained by adding the velocity of any point A of the body to the relative velocity of B with respect to A.
Second formula
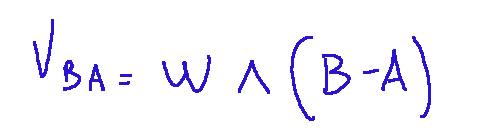
where: ω = angular velocity vector of the rigid body. ∧ = symbol for the cross product. (B-A) = position vector connecting A to B.
This second formula explains that the relative velocity between two points of a rigid body depends only on the angular velocity and the distance between the points.
Rivals' Theorem General Formula
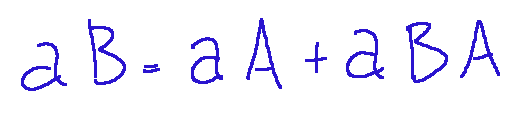
ABA Decomposition

Rivals' Theorem states that the acceleration of a point on a rigid body is given by the sum The acceleration of a reference point plus a relative part due to rotation. This theorem explains that the rotational part is decomposed into centripetal and tangential.
Conclusions The fundamental equations of motion form the basis for describing the dynamic behavior of a body under the action of forces. These equations are essential in engineering for designing and analyzing machines and structures.
Question Did you know that Rivals' theorem is named after the French engineer and mathematician Jean-Charles de Rivals de Mazères? Did you know that Rivals (1757-1828) studied applied mechanics and the dynamics of rigid bodies and clearly formalized the laws of motion in rotating systems?

ITALIAN

27-08-2025 - Meccanica - Equazioni fondamentali del moto [EN]-[IT] Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto (codice lezione/articolo: LE_90)

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione Nella meccanica applicata, le equazioni fondamentali del moto descrivono come varia la posizione, la velocità e l'accelerazione di un corpo in funzione del tempo. In questo articolo ne mostrerò qualcuna senza scendere nei dettagli, ma dando comunque una descrizione generale, in maniera da avere una sorta di raccolta di quelle più importanti e note.
Il punto di partenza dello studio delle equazioni fondamentali del moto è la legge di Newton, ovvero la seconda legge della dinamica. Essa stabilisce il legame tra forma e accelerazione. Tecnicamente la seconda legge delle dinamica esprime che la risultante delle forze applicate a un corpo è uguale al prodotto tra la massa del corpo e la sua accelerazione. Qui di seguito è mostrata la legge di cui parliamo.
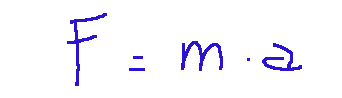
Moto traslatorio e rotatorio Ricordiamo quanto segue prima di iniziare con la serie di formule. Moto traslatorio Il moto si chiama traslatorio quando l’orientamento del corpo rimane costante. Nel moto traslatorio tutti i punti hanno la stessa velocità ed accelerazione. Moto rotatorio Abbiamo un moto rotatorio quando un corpo rigido ruota attorno ad un asse fisso e tutti i suoi punti si muovono su traiettorie circolari.
Moto rettilineo uniformemente accelerato Dalla seconda legge della dinamica derivano le relazioni cinematiche per il moto rettilineo uniformemente accelerato. Qui di seguito mostro le tre relazioni cinematiche più importanti:
Legge oraria
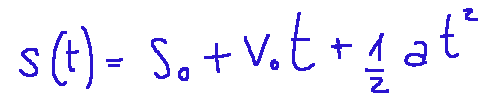
Velocità

Relazione diretta tra velocità e spazio
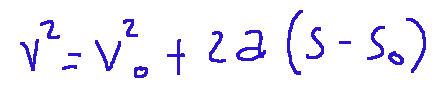
Teorema di Galileo Il teorema di Galileo ci dice che la velocità di un punto di un corpo rigido è la somma della velocità di un punto scelto più un termine legato alla rotazione.
Esso comprende due formule Prima formula
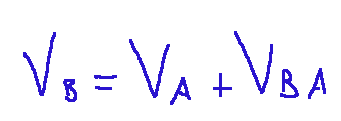
Questa formula ci dice che la velocità del punto B di un corpo rigido si ottiene sommando la velocità di un punto A qualsiasi del corpo alla velocità relativa di B rispetto ad A.
Seconda formula
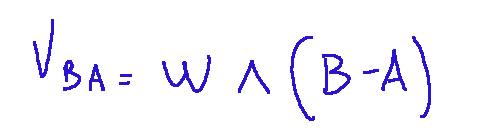
dove: ω = vettore velocità angolare del corpo rigido. ∧ = simbolo del prodotto vettoriale (B-A) = vettore posizione che unisce A con B
Questa seconda formula ci spiega che la velocità relativa tra due punti di un corpo rigido dipende solo dalla velocità angolare e dalla distanza tra i punti.
Teorema di Rivals Formula generale
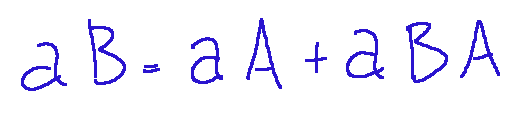
Scomposizione di aBA

Il teorema di Rivals esprime che l'accelerazione di un punto di un corpo rigido è data dalla somma dell'accelerazione di un punto di riferimento più una parte relativa dovuta alla rotazione. Questo teorema spiega che la parte relativa alla rotazione si scompone in centripeta e tangenziale.
Conclusioni Le equazioni fondamentali del moto costituiscono la base per descrivere il comportamento dinamico di un corpo sotto l’azione delle forze. Queste equazioni sono fondamentali in ingegneria per progettare e analizzare macchine e strutture.
Domanda Lo sapevate che il teorema di Rivals prende il nome dall'ingegnere e matematico francese Jean-Charles de Rivals de Mazères? Sapevate che Rivals (1757-1828) si occupò di meccanica applicata e dinamica dei corpi rigidi è formalizzò in modo chiaro le leggi del moto nei sistemi in rotazione?
THE END