
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

29-08-2025-Mechanical Measurements - Dynamic Calibration of a Second-Order Instrument [EN]-[IT] With this post, I would like to provide a brief introduction to the topic in question. (lesson/article code: LE_C-80)
Dynamic Calibration of a Second-Order Instrument

Image created with artificial intelligence, the software used is Microsoft Copilot
Introduction In the field of mechanical and thermal measurements, a second-order sensor is a sensor whose dynamic behavior is described mathematically by a second-order differential equation. Difference between a first-order and second-order sensor First-order sensor A first-order sensor is a sensor whose dynamic behavior can be described by a first-order differential equation. Its response to an input change is not immediate, but follows an exponential trend characterized by a single time constant τ. Below is the first-order model equation:
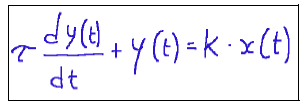
Where: y(t) = sensor output signal x(t) = input signal K = static sensitivity of the sensor τ = time constant (s), which indicates the response speed. Second-order sensor A second-order sensor is a sensor whose dynamic behavior can be described by a second-order differential equation. Essentially, when a sensor does not have an instantaneous response, but exhibits phenomena such as inertia, oscillations, or damping, it is no longer considered first-order, but second-order. Below is a typical equation for a second-order system:

Where: y(t) = sensor output signal x(t) = input quantity ωn = natural frequency (rad/s) ζ = damping coefficient y˙ (t) and y¨(t) = first and second derivatives over time
Dynamic Calibration Procedure for a Second-Order Instrument The procedure for dynamic calibration of a second-order instrument using the impulse response in the underdamped case is described below, i.e. ζ<1 starting from the fact that a second-order instrument can be described by the differential equation described below:
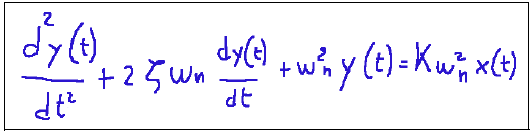
Where: y(t) = instrument output x(t) = pulse input ωn = natural frequency (rad/s) ζ = damping coefficient K = static gain
The calibration steps Dynamic
Image created with artificial intelligence, the software used is Napkin.ai
The steps for dynamic calibration of a second-order instrument are as follows: 1-Generation of the impulse input 2-Response recording 3-Response analysis 4-Calculation of dynamic parameters Below, I will attempt to describe the four steps mentioned above.
1-Generation of the impulse input The initial step consists of applying an ideal impulse to the instrument's input. Note: The impulse must be sufficiently short compared to the instrument's dynamic range. 2-Response Recording At this point, we record the instrument's output y(t) over time. 3-Response Analysis In this phase, we identify the response of oscillations with decreasing amplitude. We can measure three parameters: -The amplitude of the first peak A1 -The amplitude of the second peak A2 -The oscillation period Td
4-Calculating Dynamic Parameters The final phase is calculating the dynamic parameters, namely, damping (ζ), natural pulsation (ωn), and static gain K. Below are the mathematical formulas for the parameters described above. Damping ζ
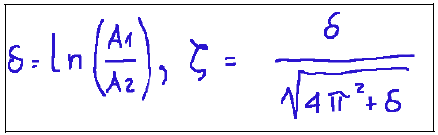
Natural Pulse ωn
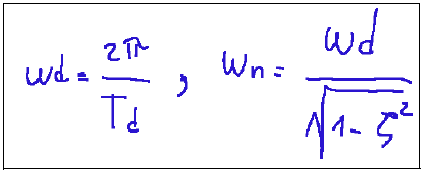
Static Gain The static gain K can be estimated from the final response value or by comparing it with the input.
Conclusions The goal of dynamic calibration is to determine characteristic parameters of an instrument by analyzing its time response to a known signal. Characteristic parameters can include: natural frequency, damping, and static gain. Compared to the dynamic calibration of a first-order instrument, the dynamic calibration of a second-order instrument requires a more in-depth analysis of the time response, the calculation of parameters such as damping and natural pulsation, and finally an understanding of the oscillatory behavior.
Question When dynamically calibrating a second-order instrument to verify the correct dynamic response, "step" tests are often used. Did you know that this means that, in practice, a simple sharp tap can reveal a lot about the dynamic behavior?

ITALIAN

29-08-2025-Misure meccaniche - Taratura dinamica di uno strumento del II ordine [EN]-[IT]** Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto (codice lezione/articolo: LE_C-80)
Taratura dinamica di uno strumento del II ordine

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione Nell’ambito delle misure meccaniche e termiche un sensore di secondo ordine è un sensore il cui comportamento dinamico viene descritto matematicamente da un’equazione differenziale del secondo ordine. Differenza tra sensore di I ordine e II ordine Sensore di I ordine Un sensore di I ordine è un sensore il cui comportamento dinamico può essere descritto da un’equazione differenziale del primo ordine. La sua risposta ad una variazione in ingresso non è immediata, ma segue un andamento esponenziale caratterizzato da una sola costante di tempo τ. Qui di seguito l’equazione del modello di primo ordine:
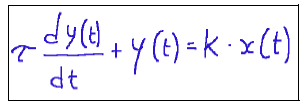
Dove: y(t)=segnale d’uscita del sensore x(t)=segnale di ingresso K=sensibilità statica del sensore τ= costante di tempo (s), la quale indica la rapidità di risposta. Sensore di II ordine Un sensore di II ordine è un sensore il cui comportamento dinamico può essere descritto da un’equazione differenziale del secondo ordine. Sostanzialmente quando un sensore non ha una risposta istantanea, ma presenta fenomeni come inerzia, oscillazioni o smorzamento, non è più considerato di I ordine, ma di secondo ordine. Qui di seguito l’equazione tipica di un sistema di II ordine:

Dove: y(t)=segnale d’uscita del sensore x(t)=grandezza di ingresso ωn=frequenza naturale (rad/s) ζ= coefficiente di smorzamento y˙ (t) e y¨(t)=derivate prima e seconda nel tempo
Procedura di taratura dinamica di uno strumento del II ordine Qui di seguito è descritta la procedura per la taratura dinamica di uno strumento del II ordine usando la risposta all’impulso nel caso sottosmorzato, cioè ζ<1 partendo dal fatto che uno strumento del II ordine può essere descritto dall’equazione differenziale descritta qui di seguito:
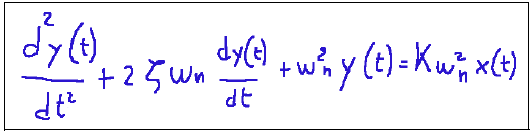
Dove: y(t)=uscita dello strumento x(t)=ingresso impulso ωn=frequenza naturale (rad/s) ζ= coefficiente di smorzamento K=guadagno statico
Le fasi della taratura dinamica

immagine creata con l’intelligenza artificiale, il software usato è Napkin.ai
Le fasi della taratura dinamica di uno strumento di II ordine sono le seguenti: 1-Generazione dell’ingresso impulsivo 2-Registrazione della risposta 3-Analisi della risposta 4-Calcolo dei parametri dinamici Qui di seguito provo a descrivere le quattro fasi citate sopra.
1-Generazione dell’ingresso impulsivo La fase iniziale consiste nell’applicare un impulso ideale all’ingresso dello strumento. Nota: L'impulso deve essere sufficientemente breve rispetto alla dinamica dello strumento. 2-Registrazione della risposta A questo punto si va a rilevare l’uscita y(t) dello strumento nel tempo 3-Analisi della risposta In questa fase si va ad identificare la risposta delle oscillazioni con ampiezza decrescente. Possiamo misurare 3 parametri: -L’ampiezza del primo picco A1 -L’ampiezza del secondo picco A2 -Il periodo di oscillazione Td
4-Calcolo dei parametri dinamici L’ultima fase è quella del calcolo dei parametri dinamici, cioè dello smorzamento (ζ), della pulsazione naturale (ωn) e del guadagno statico K Qui di seguito le formule matematiche dei parametri descritti sopra. Smorzamento ζ
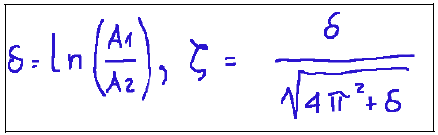
Pulsazione naturale ωn

Guadagno statico Il guadagno statico K si può stimare dal valore finale della risposta o da confronti con l’ingresso.
Conclusioni L’obiettivo della taratura dinamica è quello di determinare parametri caratteristici di uno strumento analizzando la sua risposta nel tempo a un segnale noto. I parametri caratteristici possono essere: frequenza naturale, smorzamento e guadagno statico. Rispetto alla taratura dinamica di uno strumento di I ordine, la taratura dinamica di uno strumento di II ordine richiede un’analisi più approfondita della risposta del tempo, il calcolo di parametri come lo smorzamento e la pulsazione naturale e infine la comprensione del comportamento oscillatorio.
Domanda Quando si effettua la taratura dinamica di uno strumento del II ordine per verificare la corretta risposta dinamica, si usano spesso prove con lo "scalino". Sapevate che questo significa che in pratica un semplice colpo secco racconta tantissimo sul comportamento dinamico?
THE END