
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

29-09-2025 - Operations Research - The Standard Form of an LP Problem [EN]-[IT] With this post, I would like to provide a brief introduction to the topic mentioned above. (lesson/article code: LE_C-89)

Image created with artificial intelligence, the software used is Microsoft Copilot
Introduction Linear programming, also called LP, is a mathematical method that helps a group of people make optimal decisions on problems related to cost reduction or profit maximization. Below is a linear programming problem in two variables.
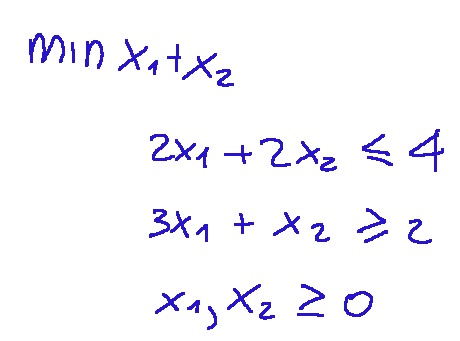
The Standard Form The first thing to do is transform the problem into standard form. The standard form is a clean and uniform form, useful because it allows you to directly apply the various methods used to solve the problem. The standard form is as follows:
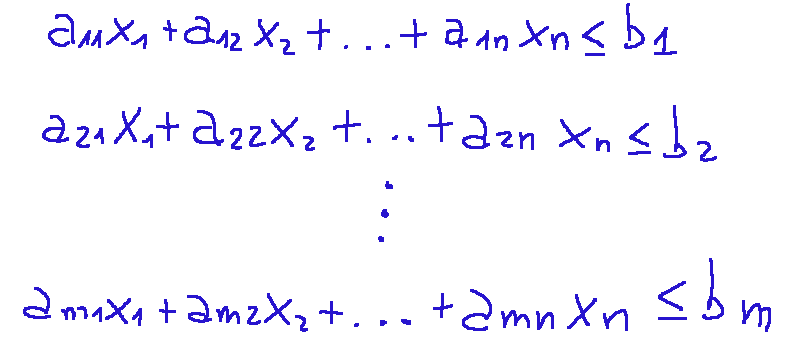
with the following final conditions:
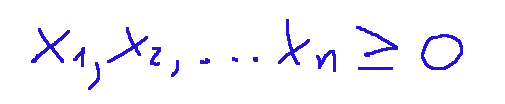
Transformation to standard form Below is our problem transformed into standard form. standard
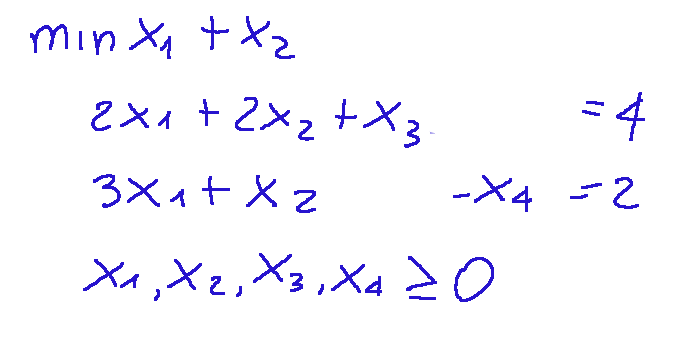
Determining A, b, and c Now we can determine the constraint coefficient matrix. Below I have highlighted the constraint coefficients, where each row corresponds to a constraint and each column to a variable.
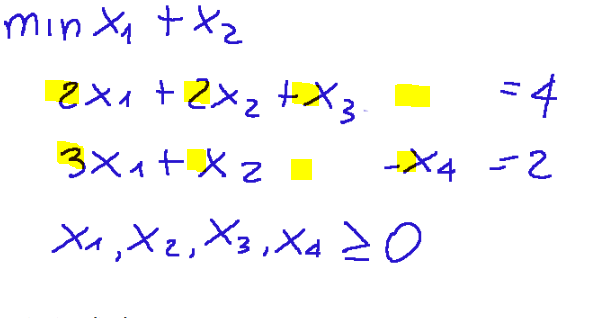
Matrix A So matrix A will be as follows:
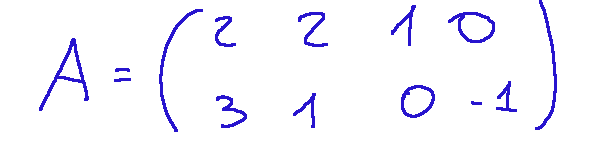
Vector b b is the vector of known terms, and these are found to the right of the constraints.
In the following image, they are highlighted.
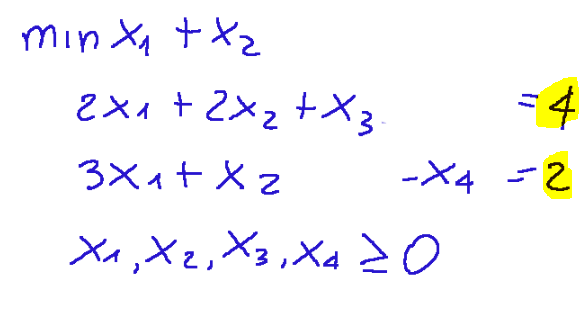
It will be transcribed like this.
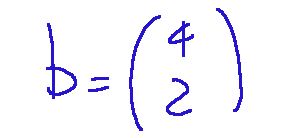
the vector c The vector c is the vector of the objective function coefficients aligned with the variables x1, x2, x3, x4. Keeping in mind that x3 and x4 do not appear, their coefficients are 0 (these are also called slack variables). Below is a screenshot to help you understand where we get them from.
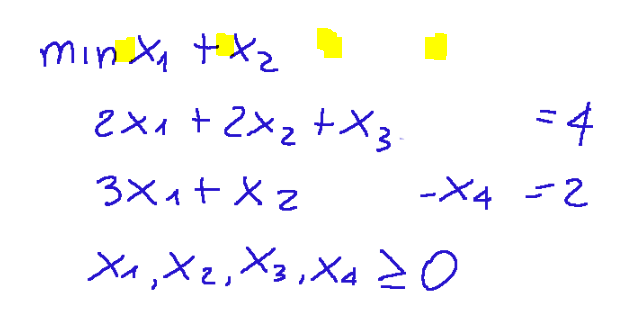
Below is the vector c.
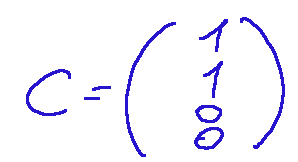
Continuation From here on, the problem can be solved in various ways, the most popular being the simplex method. This is one of those mathematical cases where problem preparation is crucial to solving the problem and obtaining the optimal solution. I will soon publish an article demonstrating a useful algorithmic method for solving this problem in standard form.
Conclusions When faced with a linear programming problem, the first thing to do is transform it into standard form so that the linear programming problem can be solved algorithmically.
Question Did you know that it was George B. Dantzig, an American mathematician and statistician, who realized that to solve a linear programming problem algorithmically, it needed to be transformed into standard form? Did you know that being able to translate a problem into a linear programming problem in standard form can be useful for solving very complex industrial production and planning problems?

ITALIAN

29-09-2025 - Ricerca operativa - La forma standard di un problema di PL [EN]-[IT] Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto (codice lezione/articolo: LE_C-89)

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione La programmazione lineare, detta anche PL, è un metodo matematico che aiuta un gruppo di persone a prendere la decisione ottima su problematiche inerenti alla riduzione dei costi o alla massimizzazione del profitto. Qui di seguito un problema di programmazione lineare in due variabili
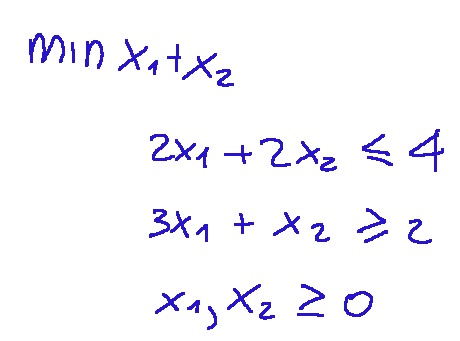
La forma standard La prima cosa da fare è trasformare il problema in forma standard. La forma standard è una scrittura pulita e uniforme, utile perché permette di applicare in modo diretto i vari metodi che si usano per risolvere il problema. L forma standard è la seguente:
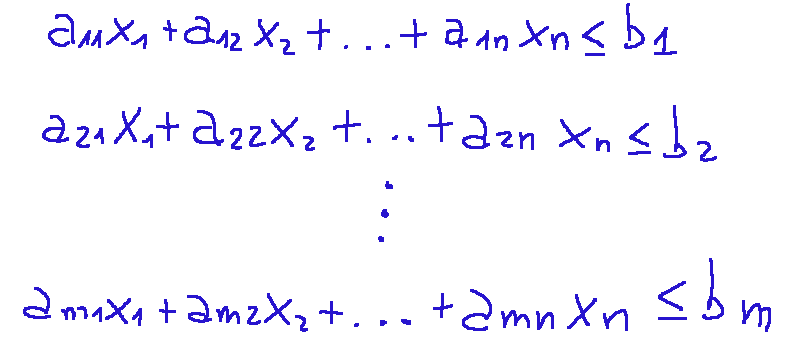
con delle condizioni finali che sono le seguenti:
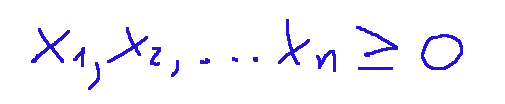
Trasformazione in forma standard Qui di seguito il nostro problema trasformato in forma standard
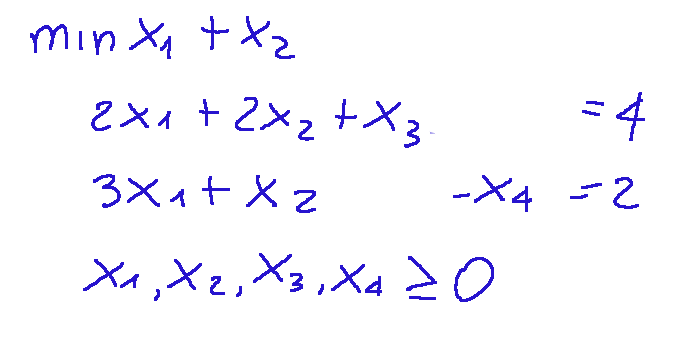
Determinazione di A, b e c Ora possiamo determinare la matrice dei coefficienti dei vincoli. Qui di seguito ho evidenziato quelli che sono i coefficienti dei vincoli, dove ogni riga corrisponde ad un vincolo e ogni colonna a una variabile
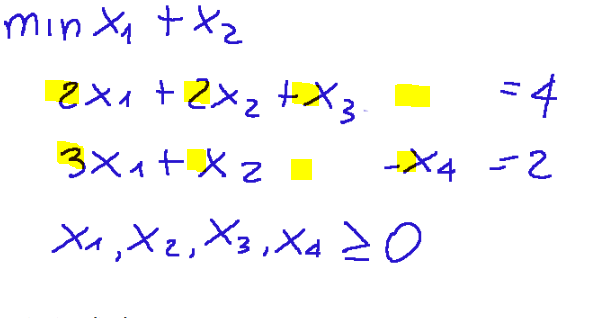
Matrice A quindi la matrice A sarà come segue:
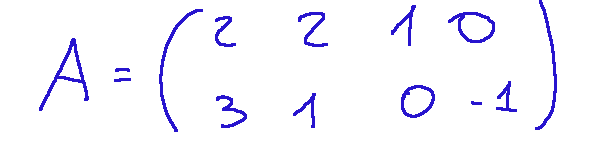
Vettore b b è il vettore dei termini noti e questi sono si trovano sulla destra dei vincoli Nell'immagine seguente sono evidenziati
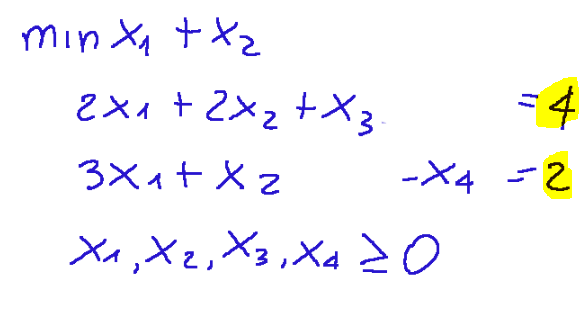
Esso sarà così trascritto
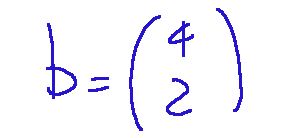
il vettore c Il vettore c è il vettore dei coefficienti della funzione obiettivo allineato alle variabili x1,x2,x3,x4. Tenendo presente che x3 e x4 non compaiono, i loro coefficienti sono 0 (queste sono anche chiamate variabili di slack). Qui di seguito allego uno screenshot per comprendere da dove le prendiamo
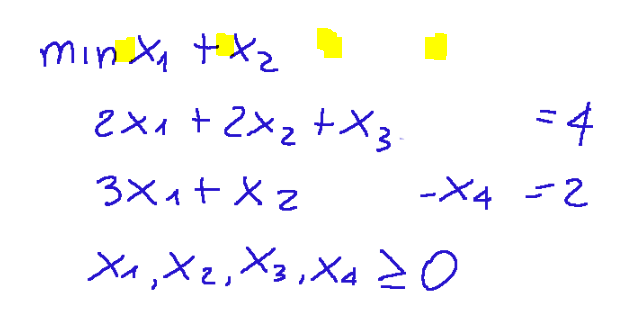
Qui di seguito il vettore c
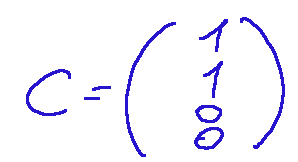
Proseguimento Da qui in poi il problema può essere risolto in vari modi, il più conosciuto è il metodo del simplesso. Questo è uno di quei casi matematici, in cui la preparazione del problema è fondamentale per risolvere il problema ed ottenere la soluzione ottima. A breve farò un articolo dove mostrerò un metodo algoritmico utile per risolvere questo problema in forma standard.
Conclusioni Di fronte ad un problema di programmazione lineare la prima cosa da fare è trasformarlo nella forma standard per fare in modo che il problema di programmazione lineare possa essere risolto tramite un algoritmo.
Domanda Sapevate che fu George B. Dantzig, un matematico e statistico statunitense, che capì che per risolvere un problema di programmazione lineare in maniera algoritmica, bisognava trasformarlo in una forma standard? Sapevate che riuscire a tradurre un problema in un problema di programmazione lineare in forma standard può essere utile a risolvere complicatissimi problemi di produzione e pianificazione industriale?
THE END