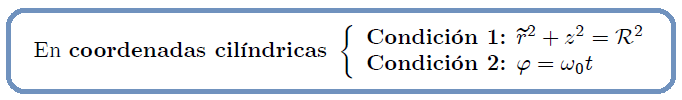Antes de todo, reciban de mi parte, un muy cordial y afectuoso saludo para todos ustedes mis estimados Steemians-Lectores, para toda la comunidad de #stem-espanol, #steemstem y el resto de la numerosa comunidad de Steemit. Como ya muchos Steemians se han enterado a través de mis publicaciones es este medio, suelo presentar posts donde intento hacer que los conceptos básicos de la Física en distintas de sus áreas sean, clara y sencillamente, bien entendidos; lo cual es enormemente importante, como suelo decirle a mis víctimas (así llamo cariñosamente a mis estudiantes), ya que si se tienen bien entendidos los conceptos básicos, entonces se entenderán con mayor claridad las teorías más complejas donde estos estén involucrados. En este post sigo evolucionando en la elaboración de mis propios gifs animados ¡espero que los disfruten!.

Este gif animado de portada fue elaborado por mi persona @tsoldovieri, usando las aplicaciones PAINT y FILMORA.
El post que les presento en esta oportunidad, mis atentos Steemians-Lectores, se trata sobre las **LIGADURAS** (constraints en inglés). Las ligaduras las estudiamos y empleamos en la carrera de Física cuando cursamos Mecánica Clásica. Su correcto entendimiento, determinación y empleo es de vital importancia al momento de estudiar la **Mecánica Lagrangiana** que fue introducida por el Matemático, Físico y Astrónomo (francés e italiano) Joseph Louis Lagrange (1736 - 1813) en 1788 (ver figura 1 - Izquierda) y la **Mecánica Hamiltoniana** que recibe su nombre del Matemático, Físico, Astrónomo y Filósofo irlandés Sir William Rowan Hamilton (1805 - 1865) (ver figura 1 - Derecha); las cuales son teorías equivalentes a la Mecánica Vectorial de Newton, pero desarrolladas a partir de fundamentos energéticos.

Figura 1: IZQUIERDA - Joseph Louis Lagrange 1736 - 1813 (De Desconocido - http://www.hrono.ru/biograf/bio_l/lagranzhzh.html, Dominio público, https://commons.wikimedia.org/w/index.php?curid=7293609 - Fuente). DERECHA - Sir William Rowan Hamilton 1805 - 1865 (By Unknown - http://www.askaboutireland.ie/search.xml?query=William+Rowan+Hamilton&radio_filter=images&type=and, Public Domain, https://commons.wikimedia.org/w/index.php?curid=11295605 - Fuente).
Mis estimados Steemians-Lectores, como algunos lo saben, la Mecánica Clásica es uno de los cursos pilares en la formación de todo futuro Físico y es un curso avanzado de la carrera, por lo que las ligaduras suelen ser estudiadas en este nivel.
Sin embargo, en el presente post, les presentaré las ligaduras de una forma tan sencilla que pueden ser estudiadas a nivel de un curso básico de Física General, sin ningún problema, lo cual sería una ventaja a la hora de estudiar Mecánica Clásica más adelante en la carrera. |
|
Se requerirá sólo de conocimientos básicos de Geometría, Trigonometría y Física General (conocimientos adquiridos en el bachillerato), los cuales supondré que están bien entendidos por cada uno de mis Steemians-Lectores, por lo que no presentaré cálculos detallados.
Bien mis atentos Steemians-Lectores, presentaré un conjunto de sistemas mecánicos sencillos y analizaré las condiciones en las que se realizan los movimientos involucrados en cada uno de ellos. Al final, lo anterior, me permitirá definir Ligadura de forma muy clara y sencilla. |
|

SISTEMA 1
**EL PENDULO SIMPLE:** observemos, mis atentos Steemians-Lectores, el péndulo simple que les muestro en la figura 2. Aquí una partícula masa 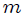 (masa pendular) cuelga de un soporte mediante una cuerda de longitud 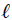, masa y elasticidad despreciable, en un campo gravitacional de intensidad 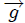, ocurriendo todo el movimiento en el plano 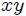. La partícula es ubicada usando un sistema de coordenadas Cartesianas, cuyo origen 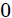 se ha colocado en el punto de soporte.
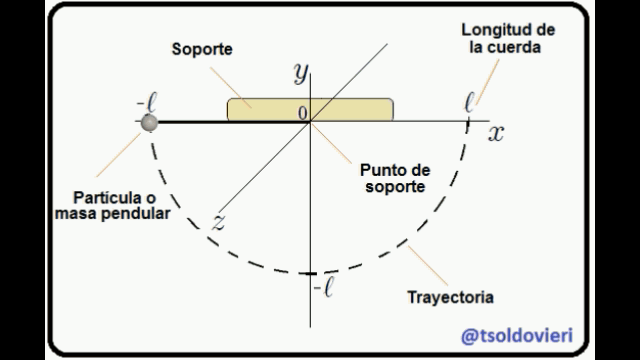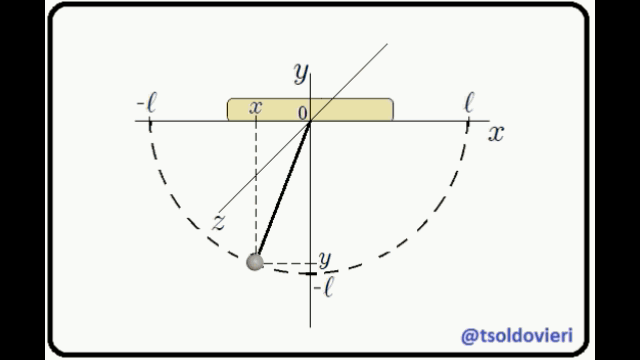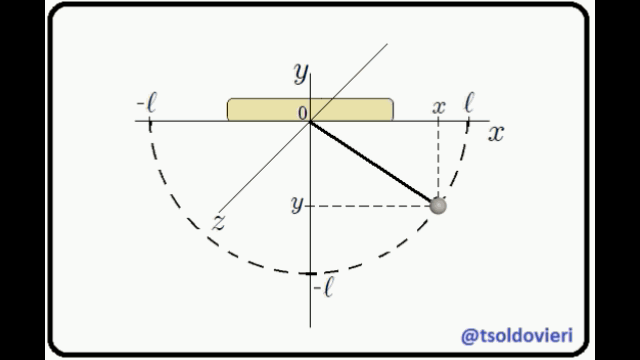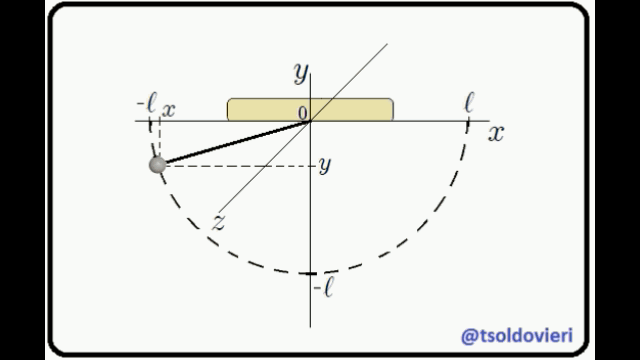
Figura 2: Péndulo Simple (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y FILMORA).
Ahora bien mis Steemians-Lectores, una partícula que es completamente libre puede moverse sin condicionamientos en todo el espacio sin problema alguno. Por el contrario, la partícula del péndulo no puede realizar un movimiento cualquiera pues debe hacerlo en el plano 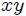, de tal forma que su distancia al punto de soporte 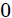 sea constante e igual a 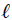. Es decir, el movimiento está condicionado. Las anteriores condiciones pueden ser expresadas matemáticamente como,

Ecuación 1
La primera condición es obvia. La segunda se obtiene al aplicar el Teorema de Pitágoras al triángulo rectángulo mostrado en la figura 3 (o a cualquiera de los triángulos que forma la cuerda con el eje 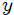).
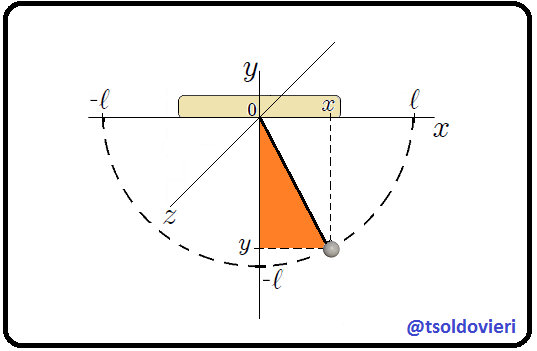
Figura 3: Péndulo Simple (Figura realizada por mi persona @tsoldovieri, usando las aplicaciones PAINT y WORD).

SISTEMA 2
**EL PLANO INCLINADO:** observemos ahora, mis estimados Steemians-Lectores, el sistema mecánico que les muestro en la figura 4. Este es el caso típico de un bloque de masa 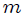 que se mueve en el plano 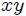, deslizándose sobre un plano inclinado.
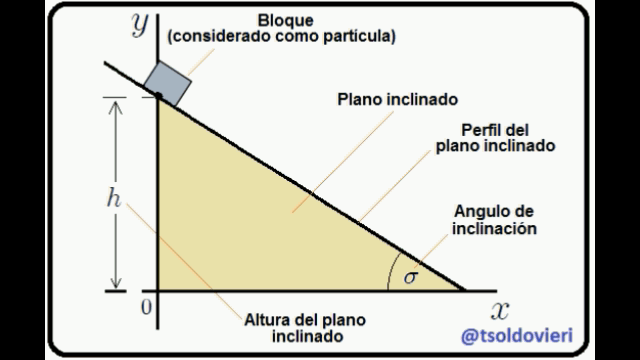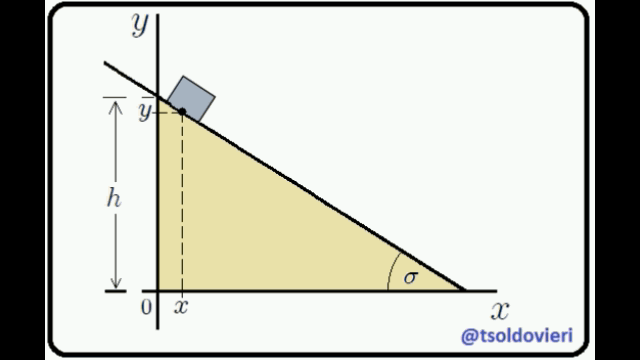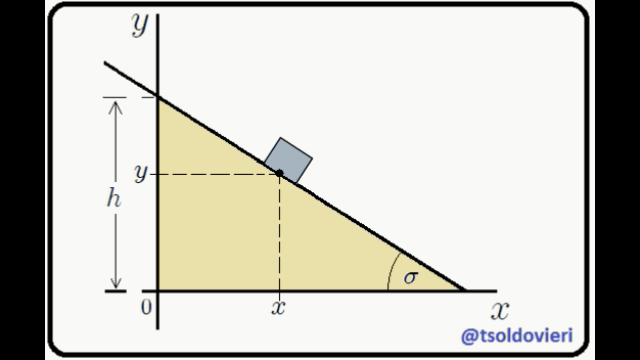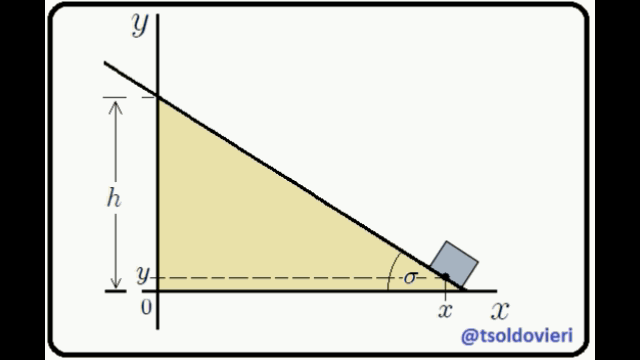
Figura 4: Bloque que se desliza sobre un plano inclinado (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y FILMORA).
El bloque está condicionado a moverse sólo en el plano 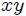 y sobre el plano inclinado. Estas condiciones pueden ser expresadas matemáticamente mediante,

Ecuación 2
La primera condición es obvia. La segunda se obtiene al encontrar la ecuación de la recta que contiene el perfil del plano inclinado, lo cual es realmente sencillo de hacer.

SISTEMA 3
**LA MAQUINA DE ATWOOD SIMPLE:** una máquina de Atwood, mis Steemians-Lectores, es un dispositivo simple compuesto por una polea (fija en su centro) por la que pasa una cuerda, de cuyos extremos penden dos cuerpos de masas 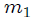 y 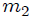. En el caso ideal, la deformación de la cuerda (elasticidad) y su masa, el tamaño de la polea y su masa, y toda posible fricción en el sistema son completamente despreciables. En la figura 5, mis Steemians-Lectores, les muestro un esquema de una máquina de este tipo, donde todo el movimiento se realiza en el plano 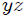 y los cuerpos son posicionados mediante el uso de un sistema de coordenadas Cartesianas, cuyo origen coincide con la posición del eje de rotación de la polea.
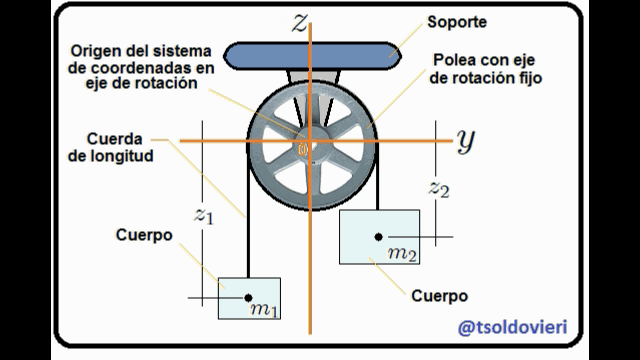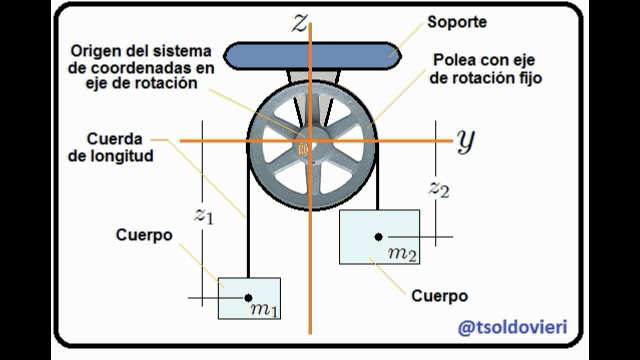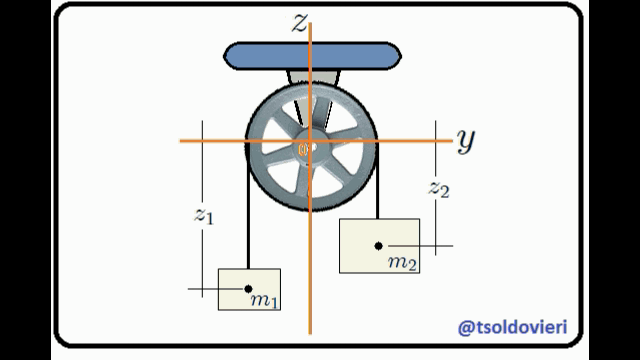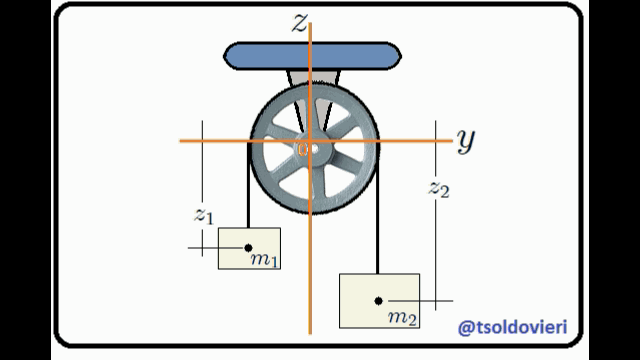
Figura 5: Máquina de Atwood Simple (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y FILMORA).
Esta máquina fue inventada en 1784 por el Físico y Matemático inglés George Atwood 1745 - 1807 (ver figura 6), como un experimento de laboratorio para verificar las leyes mecánicas del movimiento uniformemente acelerado.

Figura 6: George Atwood 1745 - 1807 (Figura tomada de la web Fisicanet, cuyo enlace es https://www.fisicanet.com.ar/biografias/cientificos/a/atwood.php - Las condiciones para utilizar contenido de esta página es citar la fuente Fisicanet y mostrar el enlace completo de la página).
El movimiento de los cuerpos 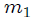 y 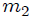 está condicionado a que se lleve a cabo sólo en el plano 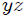. Adicionalmente a lo anterior se tiene que, debido a que el tamaño de la polea es despreciable, entonces ordenadas de la posición de cada cuerpo es nula, haciendo que ambos se muevan únicamente a lo largo del eje 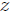. Además, debido a la cuerda, la separación entre los cuerpos se mantiene igual a la longitud 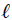 de la misma. Matemáticamente estas condiciones se pueden expresar mediante,

Ecuación 3
Las condiciones 1 y 2 son obvias. En la condición 3 no se tomó en cuenta el trozo de cuerda que pasa sobre la polea puesto que su longitud es despreciable, por ser el tamaño de la polea igualmente despreciable.

SISTEMA 4
**ESFERITA PERFORADA QUE SE DESLIZA A TRAVES DE UN ALAMBRE ROTANTE RECTO Y LISO:** mis Steemians-Lectores, en la figura 7 les muestro una esferita, de masa 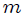 y tamaño despreciable, perforada a través de su diámetro y que puede deslizarse a través de un alambre recto y liso (de masa despreciable) que pasa por su perforación, mientas que éste rota con velocidad angular constante 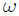. Todo el movimiento se realiza en el plano 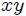. He utilizado un sistema coordenadas Cartesianas para ubicar la esferita, con origen posicionado en el eje de rotación del alambre.
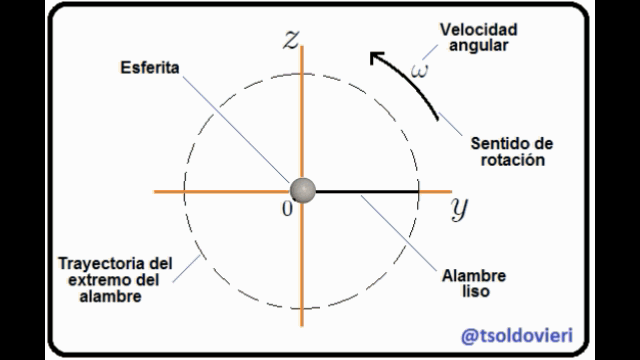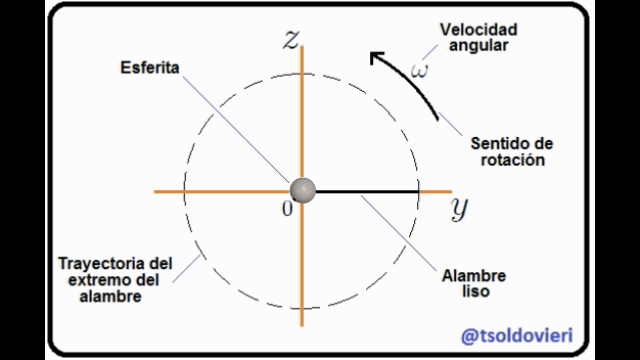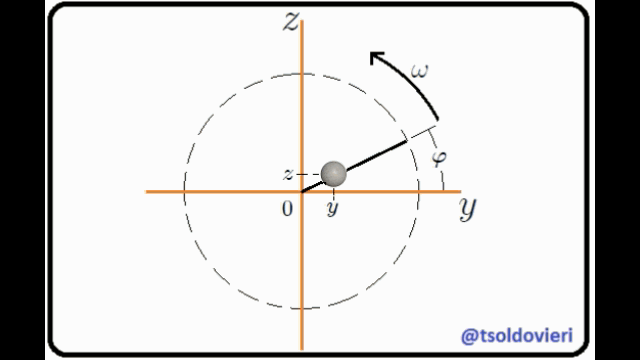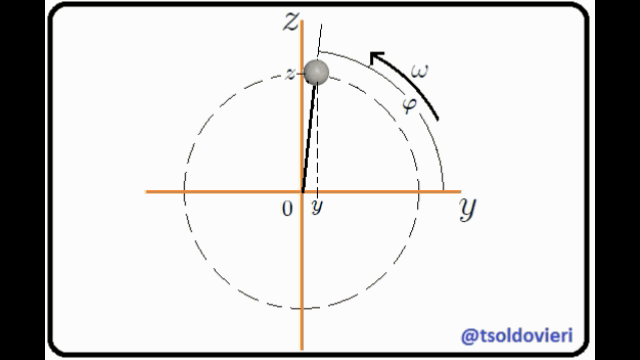
Figura 7: esferita perforada a lo largo de su diámetro, que se desliza a través de un alambre rotante recto y liso (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y FILMORA).
El movimiento de la esferita está condicionado a que sea en el plano 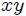 y a lo largo del alambre liso. Matemáticamente estas condiciones se pueden expresar mediante,

Ecuación 4
La condición 1 es obvia. La condición 2 viene de la ecuación de la recta que contiene al alambre.

SISTEMA 5
**ESFERITA PERFORADA QUE SE DESLIZA A TRAVES DE UN ARO LISO ROTANTE:** continuando con la presentación de sistemas mecánicos, ahora les muestro en la figura 8 un sistema formado por una esferita de radio despreciable y de masa 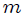 que se desliza por un aro liso de radio  y de masa despreciable, que pasa a través de un orificio en la misma. El aro gira con velocidad angular 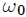 constante de manera tal que el eje de rotación pasa a través de su diámetro. En esta oportunidad, mis atentos Steemians-Lectores, he posicionado la esferita usando un sistema de coordenadas Cartesianas y un sistema de coordenadas esféricas, ambos con origen 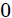 posicionado en el centro del aro.
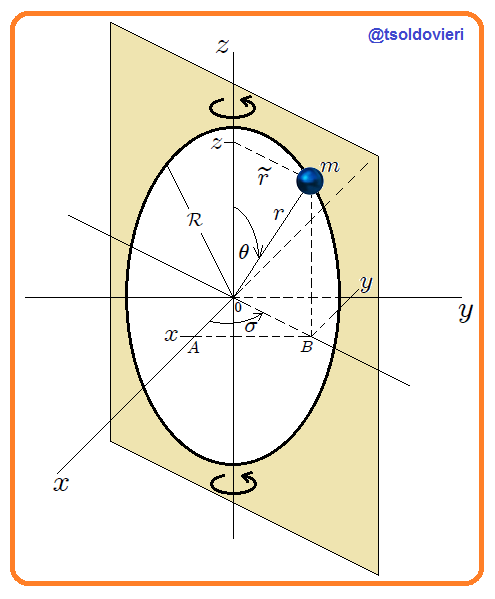
Figura 8: esferita perforada que se desliza a través de un aro liso rotante (Figura realizada por mi persona @tsoldovieri, usando las aplicaciones PAINT y WORD).
El movimiento de la esferita está condicionado a que sea a lo largo del aro y a que esté en rotación en conjunto con el mismo. Matemáticamente, en coordenadas Cartesianas, estas condiciones se pueden expresar mediante,

Ecuación 5
Las condiciones 1 y 2 se obtienen mediante simples consideraciones geométricas y trigonométricas.
En coordenadas cilíndricas y esféricas, las anteriores condiciones se pueden escribir como,
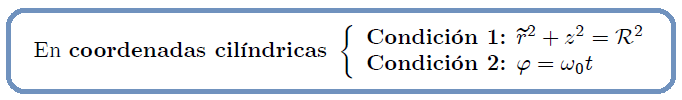
Ecuación 6

Ecuación 7
Para el caso de la coordenada radial de las coordenadas cilíndricas usé 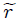 para distinguirla de la coordenada radial 23.png (https://cdn.steemitimages.com/DQmQFcsWbGSJCxPDth8DRBf4dPZEojYATCu4rQLfW1S2C3a/23.png) de las coordenadas esféricas.
linea-imagen-animada-0124.gif (https://cdn.steemitimages.com/DQmWhWr4DVbbo9kjRxkhxe3GrcKdAi53H4UF9ELDLJs1jv5/linea-imagen-animada-0124.gif)
SISTEMA 6
**MOLECULAS DE GAS ENCERRADAS EN UNA ESFERA:** en la figura 9 les muestro, atentos Steemians-Lectores, un sistema de moléculas de gas encerrado en una esfera de radio 21.png (https://cdn.steemitimages.com/DQme6hCh6K9Frvx8Y5vdNtyPEAJtuz5wCYHYxm8c9MDnQyz/21.png). He utilizado coordenadas Cartesianas, centradas en el centro de la esfera, para la ubicación de las moléculas. Los vectores 24.png (https://cdn.steemitimages.com/DQmQ1DGmGQMf3WPYqmydsFbC3Wq9CeQjd5N254mrYypFKpq/24.png) son los vectores de posición (de módulos 26.png (https://cdn.steemitimages.com/DQmZ1DWRrovUdhC252qZxMVqv2FAKeLQQv6rE6p2dtL6TiZ/26.png)) de cada una de las moléculas y 25.png (https://cdn.steemitimages.com/DQmaubspFmtdszvjqRzCik1GUAR63sUjpAUgn5rVH7TqG6u/25.png) sus masas, siendo 27.png (https://cdn.steemitimages.com/DQmURkQDpVtPnMUeGzct4Ru2yWBuuDgD8N2seZ5NU9GdVib/27.png) hasta el número total de moléculas del sistema.
MolGas.gif (https://cdn.steemitimages.com/DQmQvyNU5ctzw87yJbRoasa4aNadR5GdEf8KwkLGtpLPoEd/MolGas.gif)
Figura 9: moléculas de gas encerradas en una esfera (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y FILMORA).
Cada una de las moléculas está condicionada a moverse dentro de la esfera o sobre su superficie interna, no pudiendo salir al exterior de la misma. La anterior condición que se aplica a cada una de las moléculas puede ser escrita matemáticamente como,
28.png (https://cdn.steemitimages.com/DQmSsSJMDqNAM9L65w2xtM2AprS6z4QfiJxAQ8tDDuSeaD4/28.png)
Ecuación 8
linea-imagen-animada-0124.gif (https://cdn.steemitimages.com/DQmWhWr4DVbbo9kjRxkhxe3GrcKdAi53H4UF9ELDLJs1jv5/linea-imagen-animada-0124.gif)
SISTEMA 7
**PARTICULA QUE SE DESLIZA SOBRE LA SUPERFICIE DE UNA ESFERA LISA:** ahora, mis muy estimados Steemians-Lectores, en la figura 10 les muestro un sistema mecánico que consta de una partícula de masa 1.png (https://cdn.steemitimages.com/DQmYDv41qyP69ixGfiFQKE33xeYWS3PoRKU3FuatBFkzaqS/1.png) que se desliza sobre la superficie de una esfera lisa de radio 21.png (https://cdn.steemitimages.com/DQme6hCh6K9Frvx8Y5vdNtyPEAJtuz5wCYHYxm8c9MDnQyz/21.png). He utilizado, como en el sistema anterior, coordenadas Cartesianas centradas en el centro de la esfera para la ubicación de la partícula. El vector 29.png (https://cdn.steemitimages.com/DQmcpVMasHohgLf21rNvcp7PEFQ9gvLjuGZvqimuDFFYnHk/29.png) es el vector de posición de la partícula y