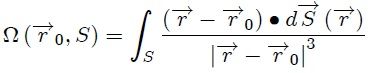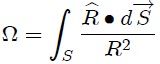Para todos los Steemians de esta gran comunidad de Steemit, cordiales y muy respetuosos saludos de mi parte!. Continuando con mi serie de posts dedicados a la definición de **ANGULO SOLIDO**, en el presente les muestro **LA EXPRESION DIFERENCIAL E INTEGRAL DEL ANGULO SOLIDO**. Todos estos posts los voy presentando de una manera pausada ya que requieren de considerable trabajo de edición de texto y creación de figuras. TODAS LAS IMAGENES AQUI PRESENTADAS SON COMPLETAMENTE DE MI AUTORIA.
INDICE DE POSTS ANTERIORES:
-
-
-
-
-
EXPRESION DIFERENCIAL E INTEGRAL DEL ANGULO SOLIDO
Supóngase ahora que se tiene una superficie plana muy pequeña 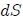, representada vectorialmente por el vector 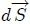 perpendicular a ella, que está situada a una distancia R de un punto fijo P y que está posicionada mediante el vector 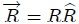 con respecto al mismo. El vector 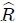 es un vector unitario en la dirección de 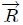, es decir, 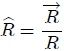.
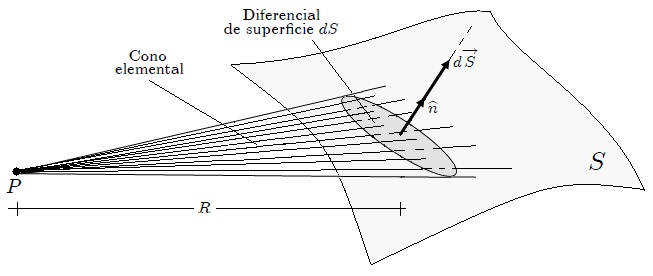
Figura 1 - Angulo sólido subtendido por una superficie diferencial 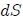 con respecto a un punto P.
con respecto a un punto P.
Gráficamente, igual que antes, el ángulo sólido subtendido por dS con respecto al punto P se obtiene al trazar semirrectas desde este punto tocando dS sin pasar por su interior, como se muestra en la figura 1. De esta manera se obtiene una superficie cónica cuya abertura interior representa el ángulo sólido buscado, superficie que suele llamársele **Cono Elemental**, por ser dS una superficie elemental o diferencial. Por la misma razón, el ángulo sólido subtendido es también elemental o diferencial y será denotado como 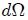.
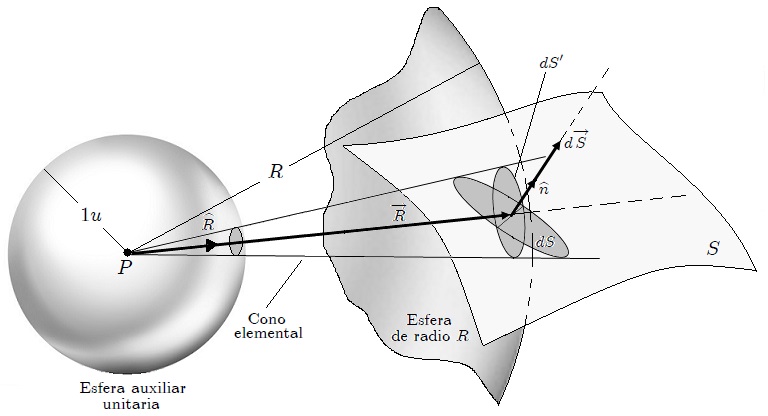
Figura 2 - Diferencial de angulo sólido 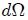 subtendido por una superficie infinitesimal
subtendido por una superficie infinitesimal 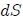 con respecto a un punto de referencia P.
con respecto a un punto de referencia P.
Para encontrar el valor numérico de 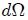 es necesario usar la definición,

Ecuación 1
vista en el post [EL ANGULO SOLIDO - PARTE 1](https://steemit.com/spanish/@tsoldovieri/el-angulo-solido-parte-1-conocimientos-basicos) y, como ya se sabe de la sección antes mencionada, debe emplearse el procedimiento representado en la figura 2. Es decir, se dibuja una esfera unitaria auxiliar con centro en P, sobre la cual el cono intercepta una superficie 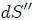 y otra esfera con centro en el mismo punto pero con radio igual a la distancia R entre P y dS, sobre la cual el cono intercepta una superficie 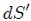. Estas dos superficies son homotéticas, siendo la segunda numéricamente igual al ángulo sólido buscado y la primera, aquella que debe ser sustituida en la ecuación 1. Entonces,
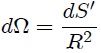
Ecuación 2
Ahora para encontrar 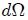 es necesario conocer el valor de 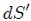, que (al igual que 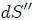) es un sector esférico diferencial. Obviamente, 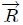 un vector normal al mismo.
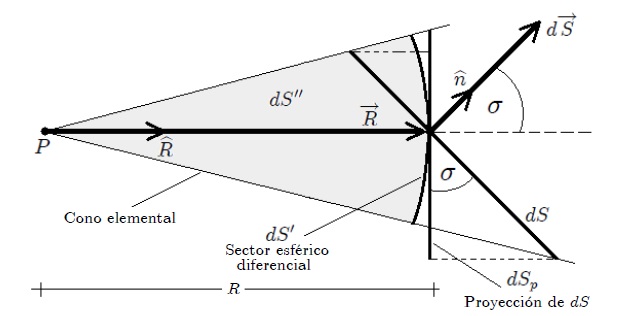
Figura 3 - Corte transversal del cono elemental de la figura 2.
Es posible aproximar, como se muestra en la figura 3, el valor de la superficie de este sector esférico (por su condición diferencial) mediante una superficie diferencial plana 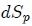 perpedicular a 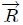 y, por ende, tangente a dicho sector,
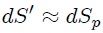
Ecuación 3
En general (La superficie 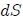 puede ser considerada esencialmente plana debido a que es muy pequeña y, por ende, es suficiente un único ángulo para indicar su orientación) la superficie 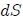 formará un ángulo 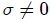 con 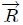 y, por lo tanto, con la 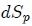. Entonces,
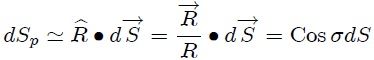
Ecuación 4
de manera que, en vista de este resultado y de la ecuación 3, la ecuación 2 puede ser escrita finalmente como,
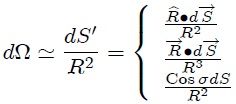
Ecuación 5
que es la expresión diferencial buscada. Para determinar el ángulo sólido subtendido por una superficie S es necesario integrar sobre toda ella la ecuación 5 resultando,
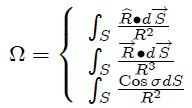
Ecuación 6
siendo la expresión integral buscada y que puede tomarse como definición formal del ángulo sólido bajo el cual se ve la superficie S desde un punto de referencia P. Aquí 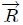 es cada vector con origen en P y extremo en un punto de cada 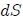.
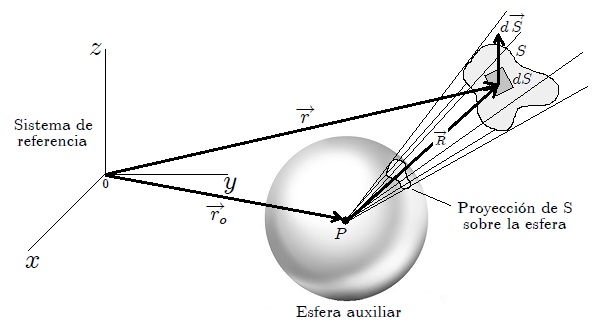
Figura 4 - Angulo sólido 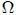 cuando P no está en el origen del sistema de coordenadas escogido.
cuando P no está en el origen del sistema de coordenadas escogido.
En el caso de que el punto P no se encuentre en el origen del sistema de coordenadas escogido sino que se encuentra a una posición 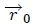 de éste (ver figura 4), el ángulo sólido vendrá dado por la expresión,
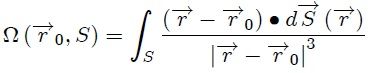
Ecuación 7
que en función del vector 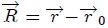 se puede escribir como,
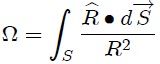
Ecuación 8
que es la misma definición dada por la ecuación 6.
El factor 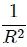 en el integrando de la ecuación 8 permite relacionar a la superficie proyectada 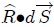 con una superficie definida en la esfera de radio unidad (esfera auxiliar) mediante una homotecia con centro en 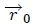, es decir, con centro en el centro de la mencionada esfera.
REFERENCIAS
-
Soldovieri, Terenzio y Viloria, Tony. EL ANGULO SOLIDO Y ALGUNA DE SUS APLICACIONES. 1era edición (borrador). Puede descargarse en mi web http://www.cmc.org.ve/tsweb/
-
Todas las imágenes aquí presentadas fueron elaboradas por mi. La imagen a color constituye una modificación de la imagen de portada del texto indicado antes, del cual soy autor.
-
Alonso, M. & Finn, E. J. FISICA - MECANICA, volume 1. Fondo Educativo Interamericano,
S.A., 1970. pp. 21 - 23 51 - 53.
-
Faget, J. & Mazzaschi, J. TEMAS PROGRAMADOS DE FISICA - GENERALIDADES, volume 1. Editorial Reverté, S.A., 1976. pp. 121 - 135.

Es mi muy sincero deseo que la anterior información les sea muy útil. Sé que dentro de la comunidad de Steemit existe una enorme cantidad de estudiantes de carreras afines a la ciencia, a los cuales esta información puede ser de gran utilidad. El próximo de esta serie se referirá a las **Propiedades del Angulo Sólido**.
Hasta mi próximo post. ¡Saludos a todos! 😁.
Si desea leer más artículos científicos de buena calidad, no pierda el tiempo, y visite la etiqueta #steemstem, es un gran proyecto que ha crecido enormemente en los últimos meses, con el fin de promover altos puestos a publicaciones científicas
Únase a nosotros en nuestro canal, también puede visitar el blog @steemstem y obtener mas información.




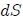 con respecto a un punto P.
con respecto a un punto P.
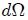 subtendido por una superficie infinitesimal
subtendido por una superficie infinitesimal 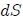 con respecto a un punto de referencia P.
con respecto a un punto de referencia P.
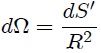

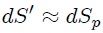
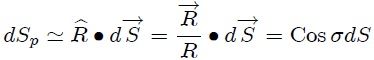
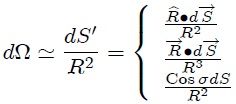
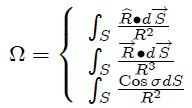

 cuando P no está en el origen del sistema de coordenadas escogido.
cuando P no está en el origen del sistema de coordenadas escogido.