Afectuosos saludos para toda la comunidad de #stem-espanol, #steemstem y el resto de la numerosa comunidad de Steemit. Particulares saludos para mis curiosos y atentos Steemians-Lectores, a los cuales aprecio mucho y estoy muy agradecido por prestarle atención a mis publicaciones. Esta vez les presento un post, referente a las denominadas **Coordenadas Generalizadas**.

Este gif animado de portada fue elaborado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape.
Para un completo entendimiento del contenido del presente post les recomiendo, a todos mis Steemians-Lectores, leer antes mi post sobre las ligaduras. |
|
Mis estimados Steemians-Lectores, las Coordenadas Generalizadas son importantísimas a la hora de estudiar:
1. **La Mecánica Lagrangiana:** introducida en 1788 por el Matemático, Físico y Astrónomo, francés e italiano, Joseph Louis Lagrange 1736 - 1813 (ver figura 1 - Izquierda).
2. **La Mecánica Hamiltoniana:** que recibe su nombre del Matemático, Físico, Astrónomo y Filósofo irlandés, Sir William Rowan Hamilton (1805 - 1865) (ver figura 1 - Derecha).

Figura 1: IZQUIERDA - Joseph Louis Lagrange 1736 - 1813 (De Desconocido - Dominio público, https://commons.wikimedia.org/w/index.php?curid=7293609 ). DERECHA - Sir William Rowan Hamilton 1805 - 1865 (By Unknown - http://www.askaboutireland.ie/search.xml?query=William+Rowan+Hamilton&radio_filter=images&type=and, Public Domain, https://commons.wikimedia.org/w/index.php?curid=11295605 ).
ya que, mis estimados Steemians-Lectores, en ambas teorías se utilizan este tipo de coordenadas para describir los sistemas mecánicos. Ambas teorías se estudian a nivel de un curso avanzado de Mecánica Clásica, por lo que las coordenadas generalizadas son introducidas a este nivel. Sin embargo, aquí les presentaré las mencionadas coordenadas de tal forma que puedan ser introducidas a nivel de un básico curso de Física General, lo cual permitiría que los estudiantes lleguen al curso avanzado de Mecánica Clásica con conocimientos previos acerca de este tema. Se requerirían sólo de conocimientos básicos de Matemática y Física, que se suponen conocidos por los estudiantes al momento de abordar este tema en un curso básico de Física General.
Para llevar a cabo el estudio o descripción de un determinado sistema mecánico es necesario conocer la posición de cada una de sus partículas (o partes que lo componen, si es un sistema donde existen cuerpos sólidos que ya no pueden ser considerados como partículas) en un instante de tiempo dado. Como todos ustedes saben, para determinar las posiciones se utilizan los Sistemas de Coordenadas. El sistema de coordenadas más sencillo y natural es el Sistema de Coordenadas Cartesianas, cuyo nombre se debe al Filósofo y científico francés **René Descartes 1596 - 1650** (ver figura 2), también conocido con el nombre latinizado de Renatus Cartesius. **Yo utilizaré, inicialmente, estas coordenadas en los sistemas mecánicos que aquí les presentaré**.

Figura 2: René Descartes 1596 - 1650 (De Según Frans Hals - André Hatala [e.a.] (1997) De eeuw van Rembrandt, Bruxelles: Crédit communal de Belgique, ISBN 2-908388-32-4., Dominio público, https://commons.wikimedia.org/w/index.php?curid=2774313 - Fuente).
Mis Steemians-Lectores (estoy pensando en llamarlos cariñosamente Steemians-Víctimas, así como llamo cariñosamente Víctimas a mis estudiantes 😁), hagámosnos ahora la siguiente pregunta: **¿Es posible describir sistemas mecánicos de tal manera que ángulos, áreas, energías, longitudes de arco, etc. puedan ser consideradas como coordenadas?**. Seguramente, a muchos de ustedes, les parecerá bastante alocada la anterior pregunta. Bueno, exploremos con algunos sistemas mecánicos sencillos a ver qué podemos obtener de ellos para poder responder a la anterior pregunta.
SISTEMA MECANICO 1
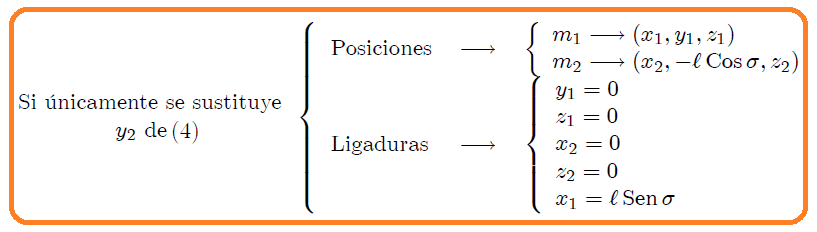
**Dos partículas de masas 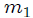 y 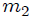 unidas por una barra rígida:** consideremos, mis atentos Steemians-Lectores, el sistema mecánico que les muestro en la figura 3, el cual está contenido por completo en el plano 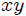. Este sistema consiste en dos partículas de masas 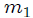 y 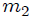 unidas por una barra rígida (cuya masa es despreciable) de longitud 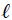, ubicadas utilizando un sistema de coordenadas Cartesianas, en el que 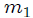 sólo se puede mover a lo largo del eje 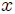 y 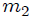 sólo a lo largo del eje 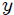.
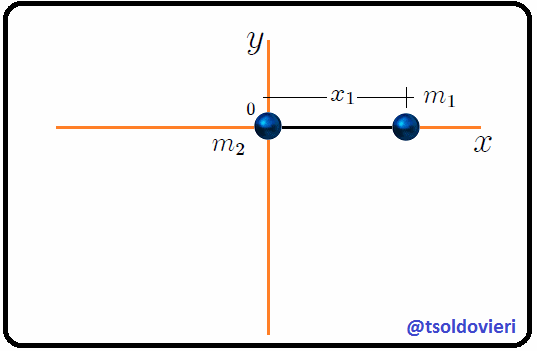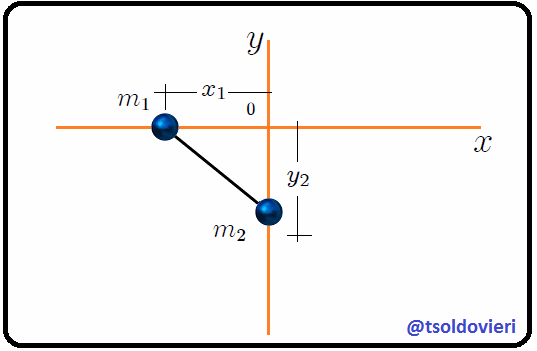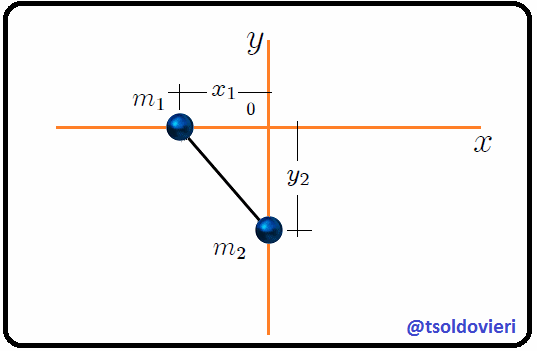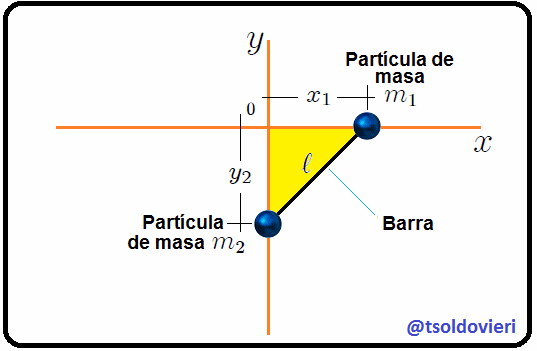
Figura 3: dos partículas de masas  y
y  unidas por una barra rígida (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
unidas por una barra rígida (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
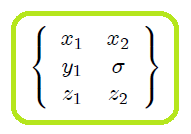
Para este sistema se tiene que las posiciones de ambas partículas y las ligaduras presentes vienen dadas por,

(1)
siendo 6 el total de coordenadas del sistema mecánico,
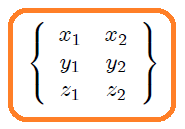
(2)
Lo anterior nos dice que, para este sistema mecánico, en las expresiones matemáticas que representan energías, ecuaciones de movimiento, fuerzas, etc., y que resultan de la descripción del mismo, estarán presentes todas o algunas de las coordenadas mostradas en (2).
Mis estimados Steemians-Lectores, consideremos ahora el mismo sistema mecánico anterior, pero con el ángulo 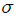 definido como les muestro en la figura 4.
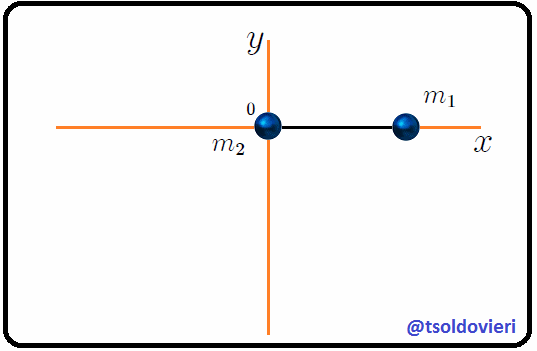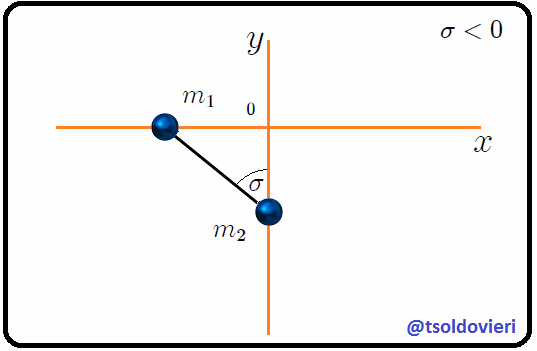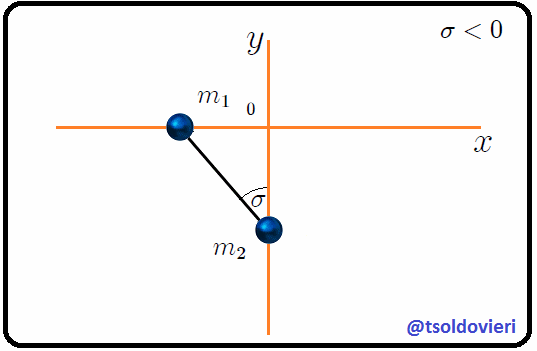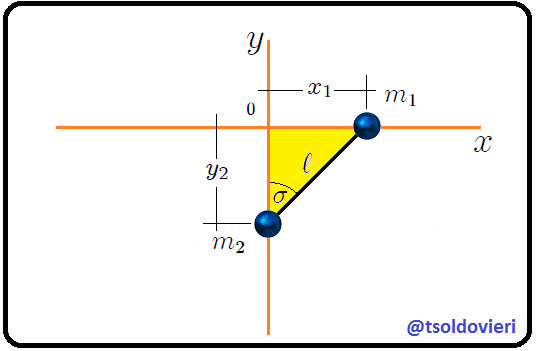
Figura 4: el mismo sistema de la figura 3 donde, ahora, se ha definido el ángulo 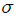 (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
(Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
Hagamos que,

(3)
lo cual nos dirá de qué lado del eje 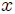 se encuentra la partícula 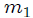 para un determinado valor de 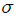. Es fácil notar que si cambiamos la posición de 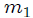 o la posición de 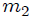, el ángulo 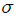 también cambiará. Lo anterior nos indica que el ángulo 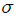 es una variable que depende del tiempo, sugiriendo que este cambio debe estar relacionado matemáticamente con el cambio de todas o algunas de las coordenadas de posición mostradas en (1). Bien mis Steemians-Lectores, del triángulo rectángulo amarillo de la figura 4 es fácil encontrar que,
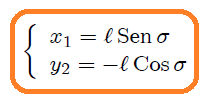
(4)
que nos muestra la relación existente entre la nueva variable 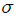 y las coordenadas 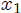 y 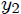. Notemos aquí que conocer el valor de 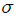 en cualquier instante de tiempo significa conocer indirectamente las coordenadas 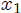 y 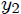. Ahora, las posiciones de ambas partículas y las ligaduras presentes podrán ser escritas como,
1. Si únicamente sustituimos 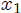 de (4) en (1):
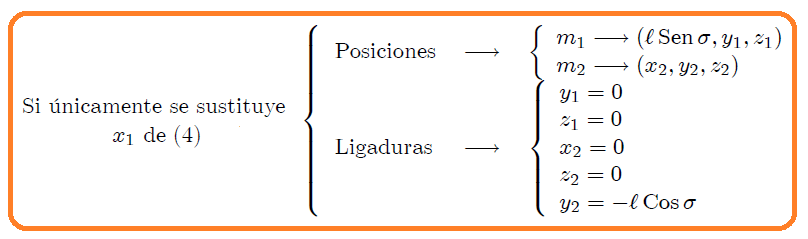
**(5)**
desapareciendo 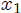, por lo que ahora tenemos un conjunto de variables formadas por las coordenadas Cartesianas restantes y la nueva variable angular 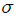,
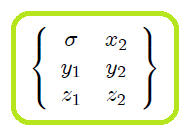
**(6)**
Lo anterior significa que todas las expresiones matemáticas que describen el sistema mecánico podrán ser escritas únicamente en función de las variables de este conjunto.
2. Si únicamente sustituimos 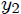 de (4) en (1):
**(7)**
siendo ahora el conjunto de variables,
**(8)**
3. Si sustituimos 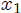 y 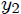 de (4) en (1):
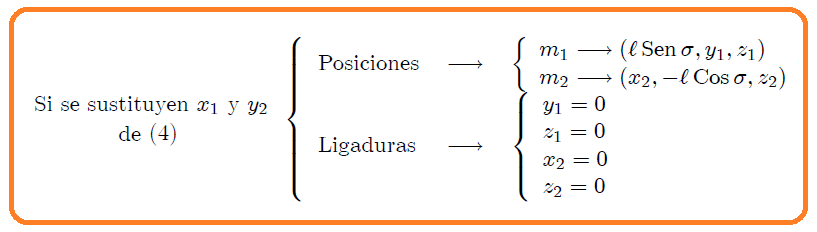
**(9)**
siendo el conjunto de variables para este caso,
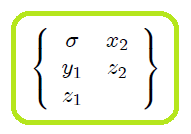
**(10)**
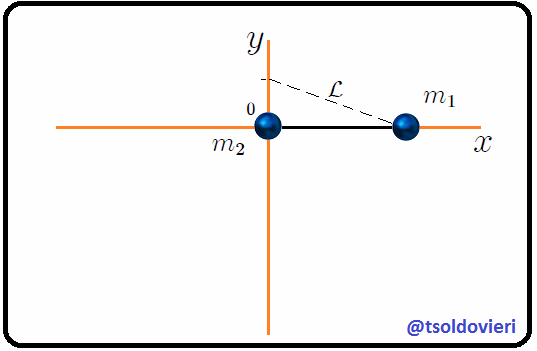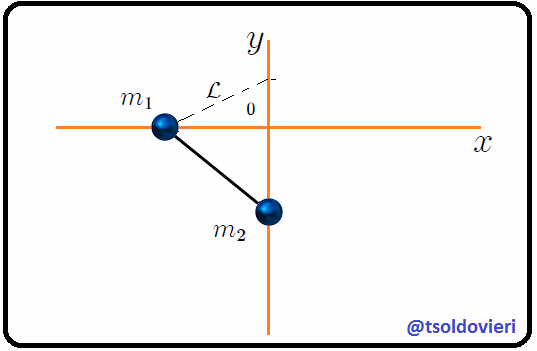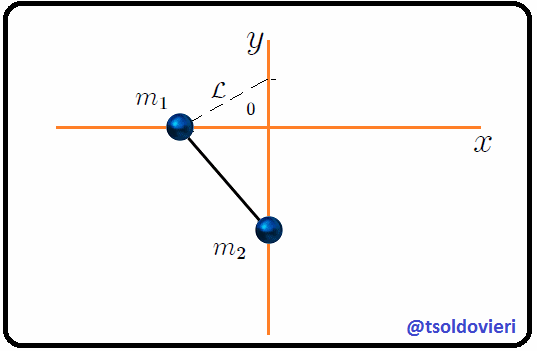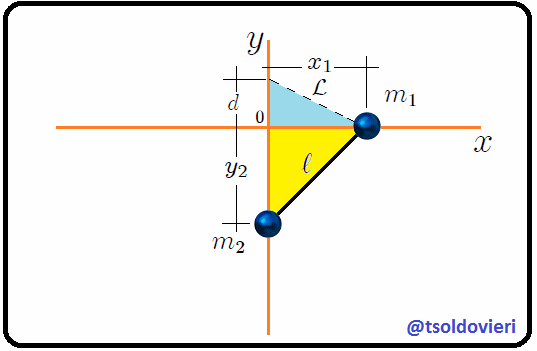
Figura 5: el mismo sistema de la figura 3 donde, ahora, se ha definido la distancia 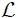 (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
(Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
Continuando con el mismo sistema mecánico, definamos ahora la distancia 18.png (https://cdn.steemitimages.com/DQmRJm6sYWXrZ52eb8fdKAPsoHDCPkSd2cqyjQZoZUpBUfd/18.png) desde un punto que está sobre el eje 4.png (https://cdn.steemitimages.com/DQmQHCT7tpbZaxeQnJFzj1QErPUiD5ohAkeacP166ngpoC6/4.png) a una distancia constante 19.png (https://cdn.steemitimages.com/DQmd2XGfE83bLY4LeoLqnzb5zzAD1pWQsVbrUZkBuqmX145/19.png) del centro de coordenadas 20.png (https://cdn.steemitimages.com/DQmc5rFYs2CF5k8AvzNAMKFrzXjjziFje2Czrfj44grgYjg/20.png) hasta la partícula 1.png (https://cdn.steemitimages.com/DQmPv3AMAr4yqPmwzB5Xn7VbDmVuHV9kVsQB8hZfS8amLeY/1.png) (como les muestro en la figura 5), de forma que,
21.png (https://cdn.steemitimages.com/DQmQf3AxVNFUGwHLSdj6UU9DsM6XBCUsjoP479vFJSxC4VJ/21.png)
(11)
Notemos, mis atentos Steemians-Lectores, que el cambio de la posición de 1.png (https://cdn.steemitimages.com/DQmPv3AMAr4yqPmwzB5Xn7VbDmVuHV9kVsQB8hZfS8amLeY/1.png) y 2.png (https://cdn.steemitimages.com/DQmZs3HsN72SWKLSJwx5yKf8apnj7QKjPjCt35G33TzmtkM/2.png) hace que 18.png (https://cdn.steemitimages.com/DQmRJm6sYWXrZ52eb8fdKAPsoHDCPkSd2cqyjQZoZUpBUfd/18.png) cambie en consecuencia, por lo tanto esta última es una variable en función del tiempo y debe estar relacionada matemáticamente con el cambio de todas o algunas de las coordenadas mostradas en (1). Efectivamente, de la figura 5, al aplicar el Teorema de Pitágoras en los triángulos rectángulos de color celeste y amarillo nos es muy fácil encontrar que,
22.png (https://cdn.steemitimages.com/DQmPMxKoSpF8a4MjQYxq6eMx4j1FZ4MPp8MDJUme19hxrqM/22.png)
(12)
que nos muestra la relación entre la nueva variable 18.png (https://cdn.steemitimages.com/DQmRJm6sYWXrZ52eb8fdKAPsoHDCPkSd2cqyjQZoZUpBUfd/18.png) y las coordenadas 9.png (https://cdn.steemitimages.com/DQmTzJy1SXR5zpoCz4cg86yij96EJToyYjyiZEyVchEbLkE/9.png) y 10.png (https://cdn.steemitimages.com/DQma1YZAebUPx452Z9KpwLLBpV2XzbKTCBFitEPLciW51Ba/10.png). Notemos mis Steemians-Lectores que conocer el valor de 18.png (https://cdn.steemitimages.com/DQmRJm6sYWXrZ52eb8fdKAPsoHDCPkSd2cqyjQZoZUpBUfd/18.png) en cualquier instante de tiempo significa conocer indirectamente las coordenadas 9.png (https://cdn.steemitimages.com/DQmTzJy1SXR5zpoCz4cg86yij96EJToyYjyiZEyVchEbLkE/9.png) y 10.png (https://cdn.steemitimages.com/DQma1YZAebUPx452Z9KpwLLBpV2XzbKTCBFitEPLciW51Ba/10.png). Si procedemos ahora como antes, las posiciones de ambas partículas y las ligaduras presentes podrán ser escritas como,
1. Si únicamente sustituimos 9.png (https://cdn.steemitimages.com/DQmTzJy1SXR5zpoCz4cg86yij96EJToyYjyiZEyVchEbLkE/9.png) de (12) en (1):
23.png (https://cdn.steemitimages.com/DQmY5aFZEtgf9UyAVyoP3ZsVxpqnqpbGbpLq6uCmYjg8ZyD/23.png)
**(13)**
por lo que ahora tenemos un conjunto de variables formadas por las coordenadas Cartesianas restantes y la nueva variable 18.png (https://cdn.steemitimages.com/DQmRJm6sYWXrZ52eb8fdKAPsoHDCPkSd2cqyjQZoZUpBUfd/18.png),
24.png (https://cdn.steemitimages.com/DQmTZ16dqJv5EsnaEfpHFEqGLeApL8ZqYavVZpTHnXqY9Cu/24.png)
**(14)**
2. Si únicamente sustituimos 10.png (https://cdn.steemitimages.com/DQma1YZAebUPx452Z9KpwLLBpV2XzbKTCBFitEPLciW51Ba/10.png) de (12) en (1):
25.png (https://cdn.steemitimages.com/DQmXG9Pe78v9n6XTHDKmEnJZcXFqo9CzWFkgdSJ3mkYYJAw/25.png)
**(15)**
siendo ahora el conjunto de variables,
26.png (https://cdn.steemitimages.com/DQmPstaBAFgrkrSiAtMxn3dr4aSm1Wfyo73WFvz6ZKQuFY2/26.png)
**(16)**
3. Si sustituimos 9.png (https://cdn.steemitimages.com/DQmTzJy1SXR5zpoCz4cg86yij96EJToyYjyiZEyVchEbLkE/9.png) y 10.png (https://cdn.steemitimages.com/DQma1YZAebUPx452Z9KpwLLBpV2XzbKTCBFitEPLciW51Ba/10.png) de (12) en (1):
27.png (https://cdn.steemitimages.com/DQmXN6tY5uxv9xx7ZjmHhBz9BcTtziXS79CJmMyAcbMfRdt/27.png)
**(17)**
siendo el conjunto de variables para este caso,
28.png (https://cdn.steemitimages.com/DQmcJJ3XP5DdnXGXp96raYgKrTyTh41hezucYpCGhGz2HdZ/28.png)
**(18)**
Observaciones1.gif (https://cdn.steemitimages.com/DQmSaiVUeRwAuCBxjEKczifTYhzqPttqFSN1T8Uxtke2vPf/Observaciones1.gif)
Mis estimados Steemians-Lectores, pudimos notar que:
1. Si formamos un conjunto con las coordenadas Cartesianas de las partículas del sistema mecánico (3 por cada partícula), nos resultará un conjunto con un número de coordenadas igual a 3 veces el número de partículas del sistema, en este caso 6 como podemos observar en (2).
2. Pudimos definir 2 variables nuevas (una a la vez): 6.png (https://cdn.steemitimages.com/DQmREUU2qxWyELJpbP4vh7Jcn2r8Cf6ksHSaxmWBPMNpcRh/6.png) y 18.png (https://cdn.steemitimages.com/DQmRJm6sYWXrZ52eb8fdKAPsoHDCPkSd2cqyjQZoZUpBUfd/18.png). Cada una de estas variables está relacionada matemáticamente con algunas de las coordenadas Cartesianas utilizadas originalmente para la ubicación de las partículas del sistema mecánico, como podemos ver en (4) y (12).
Observaciones2.gif (https://cdn.steemitimages.com/DQmdhi63LiqXqpXZXSYD2vQhAG7kQjAbtfmvLKbNPXxCwbi/Observaciones2.gif)
SISTEMA MECANICO 2
**Péndulo simple:** consideremos ahora, mis atentos Steemians-Lectores, el sistema mecánico que les muestro en la figura 6. Este sistema consiste en un péndulo simple de masa pendular 30.png (https://cdn.steemitimages.com/DQmYDv41qyP69ixGfiFQKE33xeYWS3PoRKU3FuatBFkzaqS/30.png) y longitud de la cuerda 31.png (https://cdn.steemitimages.com/DQmVWqRhsgem17inLbQkNYmdPYuoPhGiZ76Ftq3RsQukHa5/31.png). La masa pendular es ubicada utilizando un sistema de coordenadas Cartesianas, en el que la misma sólo puede moverse en el plano 29.png (https://cdn.steemitimages.com/DQmQ2hZSLdhVTdcPmJuMyVLJBisXgnJcUSU8KbwBP9rJenq/29.png).
Sistema2a.gif (https://cdn.steemitimages.com/DQme4PAT21FFB8jSxBw3fsR7e9wwm7gXEoVnEEJbDcG4vs1/Sistema2a.gif)
Figura 6: péndulo simple de masa pendular 30.png (https://cdn.steemitimages.com/DQmYDv41qyP69ixGfiFQKE33xeYWS3PoRKU3FuatBFkzaqS/30.png) y longitud de la cuerda 31.png (https://cdn.steemitimages.com/DQmVWqRhsgem17inLbQkNYmdPYuoPhGiZ76Ftq3RsQukHa5/31.png) (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
Para este sistema se tiene que la posición de la m




 y
y  unidas por una barra rígida (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
unidas por una barra rígida (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).


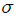 (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
(Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
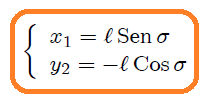

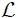 (Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).
(Gif animado realizado por mi persona @tsoldovieri, usando las aplicaciones PAINT, WORD y PhotoScape).